Question

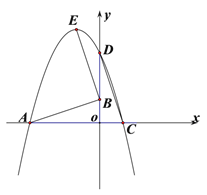
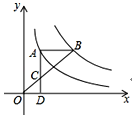
【题目】如图是反比例函数的图象，点，分别在图象的两支上，以为对角线作矩形且轴．

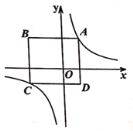
（1）当线段过原点时，分别写出与，与的一个等量关系式；

（2）当、两点在直线上时，求矩形的周长；

（3）当时，探究与的数量关系．

Answer 1

【答案】（1），；（2）矩形的周长为．（3）与的数量关系是．

【解析】

（1）根据反比例函数的对称性得到点A与点C关于原点对称，即可得到，；

（2）解两个函数关系式的方程组求出点A与点C的坐标，得到AB及BC的长，利用周长公式求出答案；

（3）由点A、C都在反比例函数的图象，得到，，根据AB=BC得到，即可求出.

（1）∵点A、C在反比例函数的图象，

∴当线段AC经过原点时，，；

（2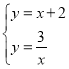），解之得，．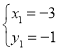

∴，．

∴，，

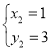∴矩形的周长=．

答：矩形的周长为．

（3）∵点、均在的图象上，

∴，．

∵，

∴．

∴．

答：与的数量关系是．