Question

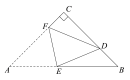
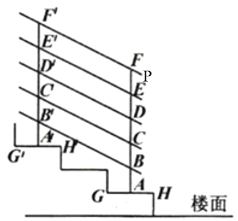
【题目】如图是楼梯一部分示意图，楼梯台阶宽度均为，高度均为，且，均与楼面垂直，点，分别是，的中点，，，．

（1）判断与的位置关系，并说明理由；

（2）求的值；

（3）求点到水平楼面的距离（精确到）．

Answer 1

【答案】（1）∥，理由见解析；（2）2；（3）

【解析】

（1）由与FB平行且相等，得出四边形是平行四边形，进而得出∥；

（2）延长、交于点K，连接，在Rt△中，求出tan∠，根据平行线的性质得出∠EFP=∠，由此得解；

（3）过点P作，交AF于点，根据的值得出与的数量关系，在Rt△中，运用勾股定理求出，进而求出到水平楼面的距离．

（1）∥，理由：

∵，均与楼面垂直

∴∥

又∵

∴=

∴四边形是平行四边形

∴∥；

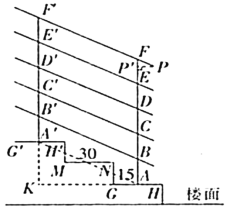
（2）如图，延长,交于点K，连接，

∵，均与楼面垂直，

∴△是直角三角形，

∵楼梯台阶宽度均为，，分别是，的中点，

∴KA=

∵楼梯高度均为，

∴

在Rt△中，tan∠=

∵∥，

∴∠EFP=∠

易证

∴∠=∠

∴tan∠EFP=tan∠=2；

（3）过点P作，交AF于点,

在Rt△中，tan∠EFP=2

∴

根据勾股定理，，即

∴cm

∴P到水平楼面的距离为16×5+15-=95-≈91.4cm．