题目内容
 如图,△AGB中,以边AG、AB为边分别作正方形AEFG、正方形ABCD,线段EB和GD相交于点H,tan∠AGB=
如图,△AGB中,以边AG、AB为边分别作正方形AEFG、正方形ABCD,线段EB和GD相交于点H,tan∠AGB=| 3 |
| 4 |
(1)求证:EB⊥GD;
(2)若∠ABE=15°,AG=
| 2 |
考点:正方形的性质,全等三角形的判定与性质,解直角三角形
专题:压轴题
分析:(1)根据正方形性质得出AG=AE,AB=AD,∠GAE=∠DAB=90°,求出∠GAD=∠EAB,根据SAS证△GAD≌△EAB,推出∠AGD=∠AEB,根据∠GAE=90°求出∠AEB+∠EMH=90°,求出∠EHM=90°,根据垂直定义推出即可;
(2)连接BD交AC于O,则AC⊥BD,根据tan∠AGB=
=
设BO=3x,则GO=4x根据GA=4x-3x=
,求出x=
求出GD=5
,BD=6
,根据△GAD≌△EAB得出BE=GD,代入求出即可.
(2)连接BD交AC于O,则AC⊥BD,根据tan∠AGB=
| 3 |
| 4 |
| BO |
| GO |
| 2 |
| 2 |
| 2 |
| 2 |
解答:(1)证明:∵四边形AEFG和四边形ACBD是正方形,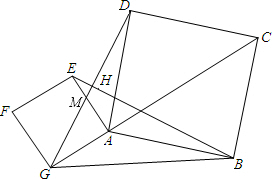
∴AG=AE,AB=AD,∠GAE=∠DAB=90°,
∴∠GAE+∠DAE=∠DAB+∠DAE,
∴∠GAD=∠EAB,
∵在△GAD和△EAB中
∴△GAD≌△EAB(SAS),
∴∠AGD=∠AEB,
∵∠GAE=90°,
∴∠AGD+∠GMA=90°,
∵∠GMA=∠EMH,
∴∠AEB+∠EMH=90°,
∴∠EHM=180°-90°=90°,
∴BE⊥DG.
(2)解:连接BD交AC于O,则AC⊥BD,
∵tan∠AGB=
=
,
设BO=3x,则GO=4x
∴GA=4x-3x=
,
∴x=
∴OD=OB=3
,OG=4
,
∴GD=5
,
由①得△GAD≌△EAB,
∴BE=GD=5
.

∴AG=AE,AB=AD,∠GAE=∠DAB=90°,
∴∠GAE+∠DAE=∠DAB+∠DAE,
∴∠GAD=∠EAB,
∵在△GAD和△EAB中
|
∴△GAD≌△EAB(SAS),
∴∠AGD=∠AEB,
∵∠GAE=90°,
∴∠AGD+∠GMA=90°,
∵∠GMA=∠EMH,
∴∠AEB+∠EMH=90°,
∴∠EHM=180°-90°=90°,
∴BE⊥DG.
(2)解:连接BD交AC于O,则AC⊥BD,

∵tan∠AGB=
| 3 |
| 4 |
| BO |
| GO |
设BO=3x,则GO=4x
∴GA=4x-3x=
| 2 |
∴x=
| 2 |
∴OD=OB=3
| 2 |
| 2 |
∴GD=5
| 2 |
由①得△GAD≌△EAB,
∴BE=GD=5
| 2 |
点评:本题考查了正方形的性质,全等三角形的性质和判定,解直角三角形等知识点的应用,主要考查学生综合运用定理进行推理和计算的能力,题目比较好,但是有一定的难度.

练习册系列答案
相关题目
 如图是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方体的块数最多是( )
如图是由一些大小相同的小正方体组成的几何体的主视图和俯视图,则组成这个几何体的小正方体的块数最多是( )| A、5 | B、6 | C、7 | D、8 |
由五个完全相同的小正方形组合而成的立体图形如图所示,它的正视图是( )

A、 |
B、 |
C、 |
D、 |
 研究表明,某种情况下,高架桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,且当0<x≤30时,V=80;当30<x≤190时,V是x的一次函数.函数关系如图所示.
研究表明,某种情况下,高架桥上的车流速度V(单位:千米/时)是车流密度x(单位:辆/千米)的函数,且当0<x≤30时,V=80;当30<x≤190时,V是x的一次函数.函数关系如图所示.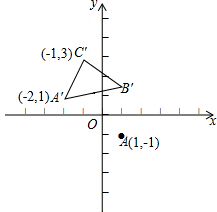 在平面直角坐标系中,△ABC的顶点A的坐标为(1,-1),平移△ABC得到△A′B′C′(如图所示),平移后点A的对应点是A′(-2,1),点C的对应点是C′(-1,3),则平移前点C的坐标为
在平面直角坐标系中,△ABC的顶点A的坐标为(1,-1),平移△ABC得到△A′B′C′(如图所示),平移后点A的对应点是A′(-2,1),点C的对应点是C′(-1,3),则平移前点C的坐标为