题目内容
9.解方程组和不等式(1)$\left\{\begin{array}{l}x-2y=6\\ 2x+3y=19\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{3}=-1}\\{3x+y=-6}\end{array}\right.$
(3)解不等式3(1-x)≥2(x+9)并把解集在数轴上表示出来.
分析 (1)加减消元法求解可得;
(2)先将方程整理成一般形式,再利用加减消元法求解可得;
(3)根据解不等式的基本步骤依次进行可得.
解答 解:(1)$\left\{\begin{array}{l}{x-2y=6}&{①}\\{2x+3y=19}&{②}\end{array}\right.$,
①×2,得:2x-4y=12 ③,
②-③,得:7y=7,
解得y=1,
将y=1代入①,得:x-2=6,
解得:x=8,
∴方程组的解为$\left\{\begin{array}{l}{x=8}\\{y=1}\end{array}\right.$;
(2)原方程组整理,得:$\left\{\begin{array}{l}{3x-2y=-6}&{①}\\{3x+y=-6}&{②}\end{array}\right.$,
②-①,得:3y=0,
解得:y=0,
将y=0代入②,得:3x=-6,
解得:x=-2,
∴方程组的解为$\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$;
(3)去括号,得:3-3x≥2x+18,
移项,得:-3x-2x≥18-3,
合并同类项,得:-5x≥15,
系数化为1,得:x≤-3,
将解集表示在数轴上如下: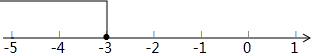
点评 本题主要考查解一元一次不等式的基本能力和解方程组的能力,严格遵循解不等式的基本步骤是关键,尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变.

练习册系列答案
相关题目
17.如果a<b,那么下列不等式成立的是( )
| A. | -3a>-3b | B. | a-3>b-3 | C. | $\frac{1}{3}$a$>\frac{1}{3}$b | D. | a-b>0 |
4.对角线长分别为6cm和8cm的菱形的面积为( )
| A. | 24cm2 | B. | 36cm2 | C. | 48cm2 | D. | 60cm2 |
14.在平面直角坐标系中,点M(-3,6)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.下列说法中,正确的是( )
| A. | 相等的角是对顶角 | |
| B. | 两条直线被第三条直线所截,内错角相等 | |
| C. | 同旁内角相等,两直线平行 | |
| D. | 平移、轴对称变换、旋转都不改变图形的形状和大小 |