题目内容
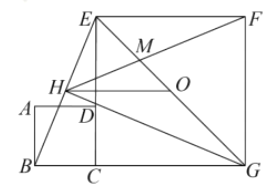
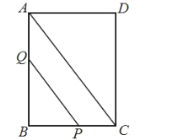
【题目】如图，在
中，
，
于
，且
.点
从点
出发，沿
方向匀速运动，速度为
；同时直线
由点
出发沿
方向匀速运动,速度为
，运动过程中始终保持
，直线交
于
，交
于
，连接
，设运动时间为
.
（1）
___________,
__________，
_____________；（用含
的式子表示）
（2）当四边形
是平行四边形时，求的值；
（3）当点在线段
的垂直平分线上时，求的值；
（4）是否存在时刻，使以为直径的圆与的边相切？若存在，直接写出的值；若不存在，请说明理由.
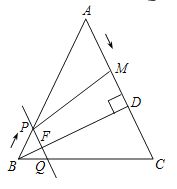
【答案】（1）
，
，
；（2）
；（3）
；（4）以
为直径的圆与
的边相切
或
或
或
.
【解析】
（1）根据题意表示出AM，即可表示出CM，证明BP=PQ，表示出BP即可，
先求出BC长，根据△BPQ∽△BAC，表示出BQ即可；
（2）当四边形
是平行四边形时，
，列出等式求解即可；
（3）当点
在线段
的垂线平分线上时，则
，分别用代数式表示出MP和MC，然后解方程即可；
（4）分①与
相切，②与
相切，③与
相切，三种情况，根据切线的性质分别求出t即可.
解：（1）点从点
出发，沿方向匀速运动，速度为
，
∴AM=2t，
∵AB=AC=10cm，
∴CM=10-2t，
∵同时直线
由点
出发沿
方向匀速运动,速度为
，
∴BP=t，
∵PQ∥AC，
∴∠PQB=∠C=∠ABC，
∴PQ=BP=t，
∵BD⊥AC，
∴∠BDA=90°，
∵BD=8cm，
∴AD=
，
∴CD=4cm，
∴BC=
，
∵PQ∥AC，
∴△BPQ∽△BAC，
∴
，即
，
∴
，
故答案为：，，；
（2）当四边形是平行四边形时，
∴
，，
即
，
解得，
∴四边形是平行四边形时，；
（3）当点在线段的垂线平分线上时，
∴，
过点作
于点
，
在
中，
，
，
，
在
中，
，
，
，
，
，
，
解得：
（舍去），
，
∴当点在线段的垂直平分线上时
；
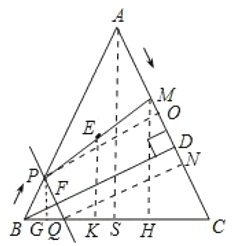
（4）存在，理由如下：
①与相切，即
时，
∴
，
∴
，
解得
；
②与相切，即
，
∴
，
∴
，
解得：
③与相切，
设圆心为E，与BC的切点为K，连接EK，则EK⊥BC，
作PG⊥BC于G，AS⊥BC于S，MH⊥BC于H，
则EK∥PG∥MH，
∵BC=，
∴BS=
，
∴AS=
，
∴
，
∴
，
∴
，
∴
，
∵E为PM的中点，
∴K为GH的中点，
∴EK为梯形PGHM的中位线，
∴
，
∴PM=2KE，
∴
解得：或；
综上，以为直径的圆与的边相切或或或.
