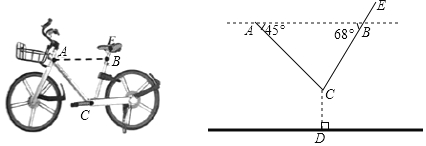
题目内容
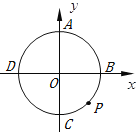
【题目】如图,半径为![]() 且坐标原点为圆心的圆交
且坐标原点为圆心的圆交![]() 轴、
轴、![]() 轴于点
轴于点![]() 、
、![]() 、
、![]() 、
、![]() ,过圆上的一动点
,过圆上的一动点![]() (不与
(不与![]() 重合)作
重合)作![]() ,且
,且![]() (
(![]() 在
在![]()
![]() 右侧)
右侧)
(1)连结![]() ,当
,当![]() 时,则点
时,则点![]() 的横坐标是______.
的横坐标是______.
(2)连结![]() ,设线段
,设线段![]() 的长为
的长为![]() ,则
,则![]() 的取值范围是____.
的取值范围是____.
【答案】±![]() ; 4
; 4![]() -4≤x≤4
-4≤x≤4![]() +4.
+4.
【解析】
(1)作PF⊥AC于点F,证明△PCF∽△ACP,可求得CF长,在Rt△PFC中求得PF的长,进而得出点P的坐标;
(2)连结OP,OE,AB,BE,AE,证明△OAP∽△BAE,可得BE= ![]() ,根据BE-OB≤OE≤BE+OB,即可得出OE的取值范围
,根据BE-OB≤OE≤BE+OB,即可得出OE的取值范围
解:(1)如图,作PF⊥AC于点F,
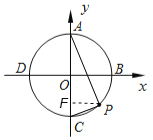
∵AB为⊙O的直径,
∴∠CFP=∠CPA=90,
∵∠PCF=∠ACP,
∴△PCF∽△ACP,
![]()
![]()
![]()
![]()
∴P点的横坐标为![]() .
.
(2)如图,连结OP,OE,AB,BE,AE,
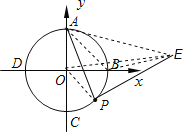
∵△AOB,△APE都为等腰直角三角形,
∴∠OAB=∠PAE=45°,![]() ,
,
∴∠OAP=∠BAE,
∴△OAP∽△BAE,
![]() ,
,
∴BE= ![]() ,
,
∵BE-OB≤OE≤BE+OB,
![]()
故答案为 ![]()

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目