题目内容
（1）x2-25=0；
（2）（x+1）3=27．
解：（1）∵x2-25=0，
∴x2=（±5）2，
∴x=±5，
（2）∵（x+1）3=27=33，
∴x+1=3，
∴x=2．
分析：（1）根据x2=b（b≥0）则x=
，（2）根据x3=a，则x=
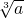，进行解答，一个数的立方根只有一个，一个数的平方根有两个，据此可以得到答案．
点评：本题考查了平方根和立方根的概念．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．立方根的性质：一个正数的立方根式正数，一个负数的立方根是负数，0的立方根式0．
∴x2=（±5）2，
∴x=±5，
（2）∵（x+1）3=27=33，
∴x+1=3，
∴x=2．
分析：（1）根据x2=b（b≥0）则x=
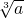，（2）根据x3=a，则x=，进行解答，一个数的立方根只有一个，一个数的平方根有两个，据此可以得到答案．点评：本题考查了平方根和立方根的概念．注意一个正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．立方根的性质：一个正数的立方根式正数，一个负数的立方根是负数，0的立方根式0．
练习册系列答案
相关题目
如图，已知AB⊥AD，CD⊥AD，垂足分别为A、D，AD=6，AB=5，CD=3，P是线段AD上的一个动点，设AP=x，DP=y，