题目内容
13.先化简,再求值:$\frac{x-1}{{x}^{2}-9}$÷($\frac{x}{x-3}$-$\frac{5x-1}{{x}^{2}-9}$),其中x=2cos30°+1.分析 先根据分式混合运算的法则把原式进行化简,再根据x=2cos30°+1求出x的值,代入原式进行计算即可.
解答 解:原式=$\frac{x-1}{(x+3)(x-3)}$×$\frac{(x-3)(x+3)}{(x-1)^{2}}$=$\frac{1}{x-1}$,
当x=2cos30°+1=$\sqrt{3}+$1时,
原式=$\frac{\sqrt{3}}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是( )
| A. | k>5 | B. | k<5 | C. | k>-5 | D. | k<-5 |
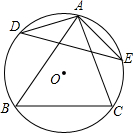 如图,△ABC内接于⊙O,∠BAC=60°,D、E分别为$\widehat{AB}$和$\widehat{AC}$的中点,连结DE.
如图,△ABC内接于⊙O,∠BAC=60°,D、E分别为$\widehat{AB}$和$\widehat{AC}$的中点,连结DE.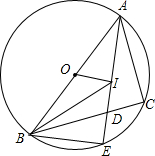 如图,△ABC内接于⊙O,AB是⊙O的直径,I是△ABC内一点,AI的延长线交BC于点D,交⊙O于E,连接BE,BI,若IB平分∠ABC,EB=EI.
如图,△ABC内接于⊙O,AB是⊙O的直径,I是△ABC内一点,AI的延长线交BC于点D,交⊙O于E,连接BE,BI,若IB平分∠ABC,EB=EI. 如图,一把折扇展开后是一个扇形,其中圆心角为120°,OB=2,AB=3,则折扇纸面部分的面积为( )
如图,一把折扇展开后是一个扇形,其中圆心角为120°,OB=2,AB=3,则折扇纸面部分的面积为( ) 如图,D是线段AB的中点,C是线段AB的垂直平分线上的一点,DE⊥AC于点E,DF⊥BC于点F.
如图,D是线段AB的中点,C是线段AB的垂直平分线上的一点,DE⊥AC于点E,DF⊥BC于点F.