题目内容
3.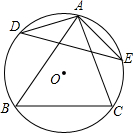 如图,△ABC内接于⊙O,∠BAC=60°,D、E分别为$\widehat{AB}$和$\widehat{AC}$的中点,连结DE.
如图,△ABC内接于⊙O,∠BAC=60°,D、E分别为$\widehat{AB}$和$\widehat{AC}$的中点,连结DE.(1)求证:BC=DE;
(2)若tan∠ADE=$\frac{1}{2}$,求sin∠AED的值.
分析 (1)根据圆周角定理得到∠E=$\frac{1}{2}$∠C,∠D=$\frac{1}{2}∠$B,求得∠D+∠E=60°,推出$\widehat{BC}=\widehat{DE}$,即可得到结论;
(2)由∠D+∠E=60°,得到tan(∠D+∠E)=tan60°=$\sqrt{3}$,根据tan(∠D+∠E)=$\frac{tan∠D+tan∠E}{1-tan∠D•tan∠E}$=$\frac{\frac{1}{2}+tan∠E}{1-\frac{1}{2}tan∠E}$=$\sqrt{3}$,解得:tan∠AED=1-2$\sqrt{3}$,将上式两边平方得求得sec∠AED=$\sqrt{14-4\sqrt{3}}$,即可得到结论.
解答 解:(1)∵D、E分别为$\widehat{AB}$和$\widehat{AC}$的中点,
∴∠E=$\frac{1}{2}$∠C,∠D=$\frac{1}{2}∠$B,
∵∠BAC=60°,
∴∠B+∠C=120°,
∴∠D+∠E=60°,
∴$\widehat{DE}$的度数=120°,
∵$\widehat{BC}$的度数=120°,
∴$\widehat{BC}=\widehat{DE}$,
∴BC=DE;
(2)∵∠D+∠E=60°,
∴tan(∠D+∠E)=tan60°=$\sqrt{3}$,
∴tan(∠D+∠E)=$\frac{tan∠D+tan∠E}{1-tan∠D•tan∠E}$=$\frac{\frac{1}{2}+tan∠E}{1-\frac{1}{2}tan∠E}$=$\sqrt{3}$,
解得:tan∠AED=1-2$\sqrt{3}$,
将上式两边平方得tan2∠AED=13-4$\sqrt{3}$,
∴sec2∠AED=tan2∠AED+1=14-4$\sqrt{3}$,
∴sec∠AED=$\sqrt{14-4\sqrt{3}}$,
∴sin∠AED=$\frac{1}{sec∠AED}$=$\frac{1}{\sqrt{14-4\sqrt{3}}}$.
点评 本题考查了三角形的外接圆和外心,圆周角定理,锐角三角函数,熟练锐角三角函数的定义是解题的关键.

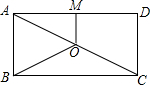 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若OM=3,AD=8,则BO=5.
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点.若OM=3,AD=8,则BO=5.