Question

13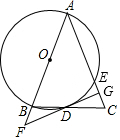．如图，在△ABC中，AB=AC，以AB为直径作⊙O交BC于点D，交AC于点E，过点D作DG⊥AC于点G，交AB的延长线于点F
（1）求证：FG是⊙O的切线；
（2）若DF=5，DG=3，求EC的长．

Answer 1

分析 （1）连接OD，AD，由圆周角定理可得AD⊥BC，结合等腰三角形的性质知BD=CD，再根据OA=OB知OD∥AC，从而由DG⊥AC可得OD⊥FG，即可得证；
（2）连接BE，先证DG为△BCE的中位线可得BE=2DG=6，CG=EG，再证△AEB∽△AGF可得$\frac{BE}{FG}=\frac{AE}{AG}$，即$\frac{AE}{AG}$=$\frac{6}{5+3}$=$\frac{3}{4}$，设EG=x，可得AE=3x，证△DGC∽△AGD可得$\frac{DG}{AG}$=$\frac{GC}{GD}$，从而求出x，根据CE=2EG可得答案．

解答 解：（1）连接OD，AD，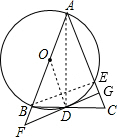

∵AB为⊙O的直径，
∴∠ADB=90°，即AD⊥BC，
∵AB=AC，
∴BD=CD，
又∵OA=OB，
∴OD∥AC，
∵DG⊥AC，
∴OD⊥FG，
∴直线FG与⊙O相切；

（2）连接BE，
∵AB为⊙O的直径，
∴BE⊥AC，
又∵DG⊥AC，
∴DG∥CE，
∵CD=BD，
∴DG为△BCE的中位线，
∴BE=2DG=6，CG=EG，
∵BE∥DG，即BE∥FG，
∴△AEB∽△AGF，
∴$\frac{BE}{FG}=\frac{AE}{AG}$，即$\frac{AE}{AG}$=$\frac{6}{5+3}$=$\frac{3}{4}$，
设EG=x，
则$\frac{AE}{AE+x}$=$\frac{3}{4}$，可得AE=3x，
∵AD⊥BC、DG⊥AC，
∴△DGC∽△AGD，
∴$\frac{DG}{AG}$=$\frac{GC}{GD}$，即$\frac{3}{4x}$=$\frac{x}{3}$，
解得：x=$\frac{3}{2}$，
∴EC=2x=3．

点评 本题主要考查圆的切线的判定、圆周角定理、相似三角形的判定与性质及中位线定理等知识点，熟练掌握圆周角定理和相似三角形的判定与性质是解题的关键．