题目内容
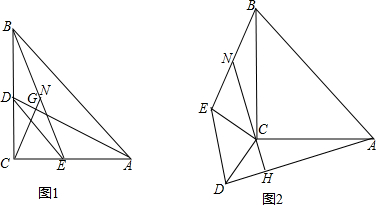
15. Rt△DEF与等腰△ABC如图放置(点A与F重合,点D,A,B在同一直线上),AD=3,AB=BC=4,∠EDF=30°,∠ABC=120°.
Rt△DEF与等腰△ABC如图放置(点A与F重合,点D,A,B在同一直线上),AD=3,AB=BC=4,∠EDF=30°,∠ABC=120°.(1)求证:ED∥AC;
(2)Rt△DEF沿射线AB方向平移,平移距离为a,当点D与点B重合时停止移动:
①当E在BC上时,求a;
②设△DEF与△ABC重叠部分的面积为S,请直接写出S与平移距离a之间的函数关系式,并写出相应的自变量a的取值范围.
分析 (1)根据已知求出∠CAD=30°,根据同位角相等进行证明即可;
(2)①过点E和点E的对应点向BD作垂线,根据平移的性质和三角函数求解即可;
②根据平移的距离判断重合部分形状,根据面积公式求解即可.
解答 解:(1)∵AB=BC,∠ABC=120°,
∴∠CAB=∠C=(180°-120°)÷2=30°,
∴∠CAB=∠EDF=30°,
∴ED∥AC;
(2)如图:
①过点E作EG⊥AD,
∵在Rt△DEF中,∠EDF=30°,DF=3,
∴DE=$\frac{3}{2}$$\sqrt{3}$EG=$\frac{3}{4}\sqrt{3}$,
∴GF=$\frac{3}{4}$,
∴a=2GF+AB=$\frac{11}{2}$;
②$S=\left\{\begin{array}{l}{\frac{\sqrt{3}}{8}{a}^{2}(0≤a≤3)}\\{\frac{9}{8}\sqrt{3}(3<a≤4)}\\{-\frac{\sqrt{3}}{4}{a}^{2}+2\sqrt{3}-\frac{23}{8}\sqrt{3}(4<a≤\frac{11}{2})}\\{\frac{\sqrt{3}}{4}{a}^{2}-\frac{7}{2}a+\frac{49}{4}\sqrt{3}(\frac{11}{2}<a≤7)}\end{array}\right.$
点评 此题主要考查平移的综合问题,会证明全等三角形,会运用平移的性质表示线段并求值,会分情况讨论表示图形面积是解题的关键.

练习册系列答案
相关题目
7.下列语句中属于命题的是( )
| A. | 相等的角是对顶角 | B. | 过点P作线段AB的垂线 | ||
| C. | 禁止抽烟! | D. | 难道是我错了吗? |
4.兴平市在“双高双普”中,为了提高全市师生阅读量,共购买图书达4640万册,4640万册用科学记数法表示为( )
| A. | 0.464×109册 | B. | 4.64×108册 | C. | 4.64×107册 | D. | 46.4×107册 |
 如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论①OH=$\frac{1}{2}$BF; ②∠CHF=45°; ③GH=$\frac{1}{4}$BC;④DH2=HE•HB中正确结论为①②④.(填序号)
如图,点O为正方形ABCD的中心,BE平分∠DBC交DC于点E,延长BC到点F,使FC=EC,连结DF交BE的延长线于点H,连结OH交DC于点G,连结HC.则以下四个结论①OH=$\frac{1}{2}$BF; ②∠CHF=45°; ③GH=$\frac{1}{4}$BC;④DH2=HE•HB中正确结论为①②④.(填序号)