题目内容
10.如图1,在等腰Rt△ACB中,∠ACB=90°,AC=BC;在等腰Rt△DCE中,∠DCE=90°,CD=CE;点D、E分别在边BC、AC上,连接AD、BE,点N是线段BE的中点,连接CN与AD交于点G.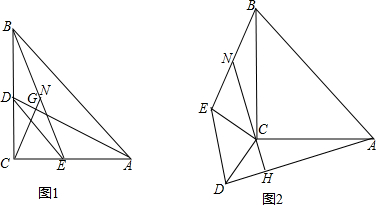
(1)若CN=6.5,CE=5,求BD的值.
(2)求证:CN⊥AD.
(3)把等腰Rt△DCE绕点C转至如图2位置,点N是线段BE的中点,延长NC交AD于点H,请问(2)中的结论还成立吗?若成立,请给出证明;若不成立,请说明理由.
分析 (1)根据直角三角形的性质得到BE=2CN=13,根据勾股定理得到BC=$\sqrt{B{E}^{2}-C{E}^{2}}$=12,即可得到结论;
(2)根据已知条件推出△ACD≌△BCE,根据全等三角形的性质得到∠CAD=∠CBE,由直角三角形的性质得到CN=BN,根据等腰三角形的性质得到∠CBE=∠NCD,等量代换得到∠NCD=∠CAD,即可得到结论;
(3)如图2,延长CN到F使FN=CN,连接BF,通过△CEN≌△BNF,得到CE=BF,∠F=∠ECN,推出∠CBF=∠DCA,证得△ACD≌△BCF,根据全等三角形的性质得到∠DAC=∠BCF,等量代换即可得到结论.
解答 解:(1)∵∠ACB=90°,点N是线段BE的中点,
∴BE=2CN=13,
∵CE=5,
∴BC=$\sqrt{B{E}^{2}-C{E}^{2}}$=12,
∵CD=CE=5,
∴BD=BC-CD=7;
(2)在△ACD与△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠ACB=90°,点N是线段BE的中点,
∴CN=BN,
∴∠CBE=∠NCD,
∴∠NCD=∠CAD,
∵∠NCD+∠NCA=90°,
∴∠CAG+∠GCA=90°,
∴∠CGA=90°,
∴CN⊥AD;
(3)(2)中的结论还成立,如图2,延长CN到F使FN=CN,连接BF,
在△CEN与△BFN中,
$\left\{\begin{array}{l}{CN=FN}\\{∠CNE=∠BNF}\\{EN=BN}\end{array}\right.$,
∴△CEN≌△BNF,
∴CE=BF,∠F=∠ECN,
∵∠CBF=180°-∠F-∠BCF,∠DCA=360°-∠DCE-∠ACB-∠BCE=180°-∠ECF-∠BCF,
∴∠CBF=∠DCA,
∵CE=CD,
∴BF=CD,
在△ACD与△BCF中,
$\left\{\begin{array}{l}{CD=BF}\\{∠ACD=∠FBC}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△BCF,
∴∠DAC=∠BCF,
∵∠BCF+∠ACH=90°,
∴∠CAH+∠ACH=90°,
∴∠AHC=90°,
∴CN⊥AD.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的性质,三角形的面积公式,正确的作出辅助线是解题的关键.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③∠AOB=150°;
④四边形AO BO′的面积为6+3$\sqrt{3}$;
⑤S△AOC+S△AOB=6+$\frac{{9\sqrt{3}}}{4}$.
其中正确的结论是( )
| A. | ①②③ | B. | ①②③④ | C. | ①②③⑤ | D. | ①②③④⑤ |
| A. | 4 | B. | 5 | C. | 6 | D. | 10 |
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 甲水果店 | 450 | 440 | 480 | 420 | 580 | 550 |
| 乙水果店 | 480 | 440 | 470 | 490 | 520 | 520 |
| A. | ax2+bx+c=0 | B. | x2+bx+c=0 | C. | x2+$\frac{b}{x}$+c=0 | D. | cx+b+x3=0 |

 Rt△DEF与等腰△ABC如图放置(点A与F重合,点D,A,B在同一直线上),AD=3,AB=BC=4,∠EDF=30°,∠ABC=120°.
Rt△DEF与等腰△ABC如图放置(点A与F重合,点D,A,B在同一直线上),AD=3,AB=BC=4,∠EDF=30°,∠ABC=120°.