题目内容
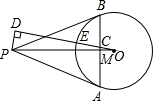 已知:如图,PA,PB分别切⊙O于点A,B,PO交AB于点M,C是MB上的一点,OC的延长线交⊙O于点E,PD⊥OE,垂足为D,且OC=3,OD=8,求⊙O的半径.
已知:如图,PA,PB分别切⊙O于点A,B,PO交AB于点M,C是MB上的一点,OC的延长线交⊙O于点E,PD⊥OE,垂足为D,且OC=3,OD=8,求⊙O的半径.
解:∵PA、PB是⊙O的切线,
∴PA=PB,∠1=∠2,
∴PO⊥AB,即∠BMO=90°,
又PD⊥OD,
∴∠PDO=90°,
∴∠BMO=∠PDO,
∵∠COM=∠DOP,
∴△OCM∽△OP′D,
∴ =
=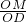 ,
,
∴OP•OM=OC•OD,
又OC=3,OD=8,
∴OP•OM=3×8=24,
∵OP是⊙O的切线,
∴OB⊥PB,
又∵PO⊥AB,
∴△OBM∽△OPB,
∴ =
=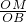 ,
,
∴OB2=OP•OM=24,
∴OB=2 ,
,
故⊙O的半径为2 .
.
分析:先利用切线的性质证明△OCM∽△OP′D,则 =
=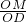 ,可以求得OP•OM,再利用切线的性质得△OBM∽△OPB,则
,可以求得OP•OM,再利用切线的性质得△OBM∽△OPB,则 =
=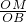 ,从而求出OB,即⊙O的半径.
,从而求出OB,即⊙O的半径.
点评:本题考查了相似三角形的判定和性质,切线的性质,切线长定理等知识,综合性强,难度较大.
∴PA=PB,∠1=∠2,
∴PO⊥AB,即∠BMO=90°,
又PD⊥OD,
∴∠PDO=90°,
∴∠BMO=∠PDO,
∵∠COM=∠DOP,
∴△OCM∽△OP′D,
∴
 =
=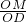 ,
,∴OP•OM=OC•OD,
又OC=3,OD=8,
∴OP•OM=3×8=24,
∵OP是⊙O的切线,
∴OB⊥PB,
又∵PO⊥AB,
∴△OBM∽△OPB,
∴
 =
=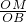 ,
,∴OB2=OP•OM=24,
∴OB=2
 ,
,故⊙O的半径为2
 .
.分析:先利用切线的性质证明△OCM∽△OP′D,则
 =
=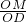 ,可以求得OP•OM,再利用切线的性质得△OBM∽△OPB,则
,可以求得OP•OM,再利用切线的性质得△OBM∽△OPB,则 =
=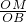 ,从而求出OB,即⊙O的半径.
,从而求出OB,即⊙O的半径.点评:本题考查了相似三角形的判定和性质,切线的性质,切线长定理等知识,综合性强,难度较大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
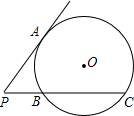 已知:如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=2PB,求
已知:如图,PA是圆的切线,A为切点,PBC是圆的割线,且BC=2PB,求 23、已知:如图,PA、PB是⊙O的切线;A、B是切点;连接OA、OB、OP,
23、已知:如图,PA、PB是⊙O的切线;A、B是切点;连接OA、OB、OP, 于点D、E.
于点D、E. 已知:如图,PA,PB分别与⊙O相切于A,B点,C为⊙O上一点,∠ACB=65°,则∠APB等于( )
已知:如图,PA,PB分别与⊙O相切于A,B点,C为⊙O上一点,∠ACB=65°,则∠APB等于( ) 已知:如图,PA切⊙O于A点,PO交⊙O于B点.PA=15cm,PB=9cm.求⊙O的半径长.
已知:如图,PA切⊙O于A点,PO交⊙O于B点.PA=15cm,PB=9cm.求⊙O的半径长.