题目内容
如图，在△ABC中，D为BC边的中点，E为AC边上的任意一点，BE交AD于点O，且| AE |
| EC |
| 1 |
| n |
| AO |
| OD |
考点：平行线分线段成比例
专题：
分析：过D作DF∥BE，根据平行线分线段成比例定理，可得出AO：AD=AE：AF，由已知
=
，可得出
=
，从而得出AE：EF=2：n，根据
=
，得出答案AO：OD=2：n．
| AE |
| EC |
| 1 |
| n |
| AE |
| AC |
| 1 |
| n+1 |
| AE |
| EF |
| AO |
| OD |
解答：
解：过D作DF∥BE，
∴AO：AD=AE：AF．
∵D为BC边的中点，
∴CF=EF=0.5EC．
∵
=
，
∴
=
，
即AE：（AE+2EF）=1：（1+n），
∴AE+2EF=AE+AEn，
∴AEn=2EF，
∴AE：EF=2：n．
∵
=
，
∴AO：OD=2：n．
解：过D作DF∥BE，∴AO：AD=AE：AF．
∵D为BC边的中点，
∴CF=EF=0.5EC．
∵
| AE |
| EC |
| 1 |
| n |
∴
| AE |
| AC |
| 1 |
| n+1 |
即AE：（AE+2EF）=1：（1+n），
∴AE+2EF=AE+AEn，
∴AEn=2EF，
∴AE：EF=2：n．
∵
| AE |
| EF |
| AO |
| OD |
∴AO：OD=2：n．
点评：本题考查了平行线分线段成比例定理，本题辅助线的作法是解题的关键．
练习册系列答案
相关题目
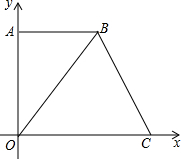如图，在平面直角坐标系中，点O是坐标原点，四边形AOCB是梯形，AB∥OC，点A的坐标为（0，8），点C的坐标为（10，0），OB=OC．
如图，圆O的半径为5，PA，PB是圆O的切线，切点分别为A，B，∠APB=90°，则PA=
如果（x+m）（x-n）中不含x的一次项，则m、n满足（ ）
| A、m=n | B、m=0 |
| C、m=-n | D、n=0 |