题目内容
解方程:2x2-4x+4=5.
考点:解一元二次方程-配方法
专题:
分析:用配方法解一元二次方程的步骤:
①把原方程化为ax2+bx+c=0(a≠0)的形式;
②方程两边同除以二次项系数,使二次项系数为1,并把常数项移到方程右边;
③方程两边同时加上一次项系数一半的平方;
④把左边配成一个完全平方式,右边化为一个常数;
⑤如果右边是非负数,就可以进一步通过直接开平方法来求出它的解,如果右边是一个负数,则判定此方程无实数解.
①把原方程化为ax2+bx+c=0(a≠0)的形式;
②方程两边同除以二次项系数,使二次项系数为1,并把常数项移到方程右边;
③方程两边同时加上一次项系数一半的平方;
④把左边配成一个完全平方式,右边化为一个常数;
⑤如果右边是非负数,就可以进一步通过直接开平方法来求出它的解,如果右边是一个负数,则判定此方程无实数解.
解答:解:2x2-4x+4=5,
移项得2x2-4x-1=0,
二次项系数化为1,得x2-2x=
,
配方,得x2-2x+1=
+1,
即(x-1)2=
,
开方得x-1=±
,
x1=1+
,x2=1-
.
移项得2x2-4x-1=0,
二次项系数化为1,得x2-2x=
| 1 |
| 2 |
配方,得x2-2x+1=
| 1 |
| 2 |
即(x-1)2=
| 3 |
| 2 |
开方得x-1=±
| ||
| 2 |
x1=1+
| ||
| 2 |
| ||
| 2 |
点评:此题考查了配方法解一元二次方程,解题时要注意解题步骤的准确应用.选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
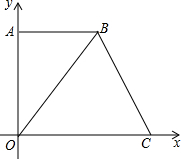 如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC.
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AB∥OC,点A的坐标为(0,8),点C的坐标为(10,0),OB=OC.