题目内容
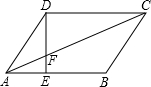
 如图,平行四边形DEFG内接于△ABC,已知△ADE,△EFC,△DBG的面积为1,3,1,那么?DEFG的面积为
如图,平行四边形DEFG内接于△ABC,已知△ADE,△EFC,△DBG的面积为1,3,1,那么?DEFG的面积为
- A.2

- B.2
- C.3
- D.4
D
分析:作三角形的高AM⊥BC,交DE与N,交BC于M,求出平行线分割的高线的分割比例即可.
解答: 解:作三角形的高AM⊥BC,交DE与N,交BC于M,如图:
解:作三角形的高AM⊥BC,交DE与N,交BC于M,如图:
设AN=1,MN=x.
∵△ADE的面积为1.
∴FG=DE=2,?DEFG的面积为2x;
又∵DE∥BC,
∴△ADE∽△ABC,
根据面积之比等于高的比的平方,
∴S△ADE:S△ABC=1:(5+2x)=12:(1+x)2,
解得x=2,
故?DEFG的面积为4.
故选D.
点评:本题结合三角形的知识综合考查了平行四边形的性质,解题关键是利用平行四边形的性质结合相似三角形来解决有关的计算.
分析:作三角形的高AM⊥BC,交DE与N,交BC于M,求出平行线分割的高线的分割比例即可.
解答:
 解:作三角形的高AM⊥BC,交DE与N,交BC于M,如图:
解:作三角形的高AM⊥BC,交DE与N,交BC于M,如图:设AN=1,MN=x.
∵△ADE的面积为1.
∴FG=DE=2,?DEFG的面积为2x;
又∵DE∥BC,
∴△ADE∽△ABC,
根据面积之比等于高的比的平方,
∴S△ADE:S△ABC=1:(5+2x)=12:(1+x)2,
解得x=2,
故?DEFG的面积为4.
故选D.
点评:本题结合三角形的知识综合考查了平行四边形的性质,解题关键是利用平行四边形的性质结合相似三角形来解决有关的计算.

练习册系列答案
相关题目
 如图,平行四边形ABCD中,E是AB上一点,DE与AC交于点F,且S△AEF=6cm2,S△DCF=54cm2,则S平行四边形ABCD=
如图,平行四边形ABCD中,E是AB上一点,DE与AC交于点F,且S△AEF=6cm2,S△DCF=54cm2,则S平行四边形ABCD= 已知:如图,平行四边形ABCD中,E是BC中点,连接DE并延长,与AB的延长线交于点F.
已知:如图,平行四边形ABCD中,E是BC中点,连接DE并延长,与AB的延长线交于点F. 24、如图,平行四边形ABCD中,BE、DF分别垂直AC于E、F,猜想DE等于BF吗?试说明理由.
24、如图,平行四边形ABCD中,BE、DF分别垂直AC于E、F,猜想DE等于BF吗?试说明理由. 如图,平行四边形ABCD中,∠A=130°,CD=DE,则∠ECB=
如图,平行四边形ABCD中,∠A=130°,CD=DE,则∠ECB= 如图,平行四边形中,∠ABC=75°.AF⊥BC于F,AF交BD于E,若DE=2AB,则∠AED=
如图,平行四边形中,∠ABC=75°.AF⊥BC于F,AF交BD于E,若DE=2AB,则∠AED=