题目内容
7.已知不等式组$\left\{\begin{array}{l}{2(x-a)<2}&{①}\\{x-3b>3}&{②}\end{array}\right.$的解集为-2<x<1,求(a+1)(b-1)的值.分析 首先解不等式组求得不等式组的解集,然后根据解集为-2<x<1,得到关于a、b的方程组求得a和b的值,进而求得代数式的值.
解答 解:解①得:x<a+1,
解②得:x>3b+3,
则不等式组的解集是:3b+3<x<a+1,
则$\left\{\begin{array}{l}{3b+3=-2}\\{a+1=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=0}\\{b=-\frac{5}{3}}\end{array}\right.$.
则(a+1)(b-1)=-$\frac{5}{3}$-1=-$\frac{8}{3}$.
点评 本题考查的是一元一次不等式组的解,解此类题目常常要结合数轴来判断.还可以观察不等式的解,若x>较小的数、<较大的数,那么解集为x介于两数之间.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.融侨半岛某文具店购入一批笔袋进行销售,进价为每个20元,当售价为每个50元时,每星期可以卖出100个,现需降价处理:售价每降价3元,每星期可以多卖出15个,店里每星期笔袋的利润要达到3125元.若设店主把每个笔袋售价降低x元,则可列方程为( )
| A. | (30+x)(100-15x)=3125 | B. | (30-x)(100+15x)=3125 | ||
| C. | (30+x)(100-5x)=3125 | D. | (30-x)(100+5x)=3125 |
12.$\frac{3}{4}$的相反数是( )
| A. | -1$\frac{1}{3}$ | B. | -|-$\frac{3}{4}$| | C. | -(-1$\frac{1}{3}$) | D. | |-$\frac{3}{4}$| |
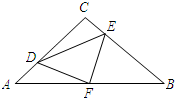 如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF
如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持AD=CE.连接DE、DF、EF
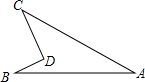 如图,∠BDC=98°,∠ACD=38°,∠ABD=23°,则∠A的度数是37°.
如图,∠BDC=98°,∠ACD=38°,∠ABD=23°,则∠A的度数是37°.