题目内容
5.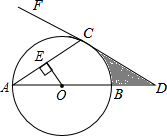 已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D.
已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D.(1)求证:FD是⊙O的切线;
(2)设AC=4$\sqrt{3}$,OE=2,求图中阴影部分的面积.(结果保留根号)
分析 (1)连接OC,根据OA=OC得出∠OAC=∠OCA,再利用∠FCA=∠AOE,再利用∠FCA=∠AOE和∠AEO=90°,得∠ACO=90°,即可证明FD是⊙O的切线;
(2)根据三角函数的定义即可得出∠A的度数,则∠COD=2∠A,阴影部分的面积=三角形COD的面积-扇形BOC的面积.
解答  (1)证明:连接OC,
(1)证明:连接OC,
∵OA=OC,
∴∠A=∠ACO,
∵OE⊥AC,∠FCA=∠AOE,
∴∠A+∠AOE=∠ACO+∠FCA=90°,
∴∠FCO=90°,
∴FD是⊙O的切线;
(2)解:∵OE⊥AC,
∴AE=CE,
∵AC=4$\sqrt{3}$,
∴AE=2$\sqrt{3}$,
∵OE=2,
∴OA=4,
∴∠A=30°,
∴∠COB=60°,
∴∠D=30°,
∴CD=4$\sqrt{3}$,
∴S阴影=S△OCD-S扇形BOC
=$\frac{1}{2}$CO•CD-$\frac{60π•{4}^{2}}{360}$
=$\frac{1}{2}$×4×4$\sqrt{3}$-$\frac{8}{3}$π
=8$\sqrt{3}$-$\frac{8}{3}$π.
点评 本题考查了扇形面积的计算、切线的判定与性质,证明一条直线为圆的切线,连接切点和圆心,再证明垂直是解题的关键.

练习册系列答案
相关题目
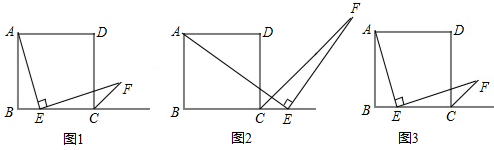
 如图△ABC中,点D是AC中点,点E在AB上,且∠B=90°,若DE=$\frac{1}{2}$AB,则命题:“DE是△ABC的中位线”是否正确?若正确,请说明理由;若不正确,请举例说明.
如图△ABC中,点D是AC中点,点E在AB上,且∠B=90°,若DE=$\frac{1}{2}$AB,则命题:“DE是△ABC的中位线”是否正确?若正确,请说明理由;若不正确,请举例说明. 如图:
如图: 已知,如上右图,动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=-x+1相交于点E,F,则AF•BE的值是( )
已知,如上右图,动点P在函数y=$\frac{1}{2x}$(x>0)的图象上运动,PM⊥x轴于点M,PN⊥y轴于点N,线段PM、PN分别与直线AB:y=-x+1相交于点E,F,则AF•BE的值是( )
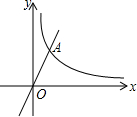 已知图中的曲线为反比例函数y=$\frac{k+2}{x}$(k为常数)的图象的一支.
已知图中的曲线为反比例函数y=$\frac{k+2}{x}$(k为常数)的图象的一支.