题目内容
2.若$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{5}$(abc≠0),求$\frac{a+b+c}{a-b+c}$的值.分析 先设$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{5}$=k,可得a=2k,b=3k,c=5k,再把a、b、c的值都代入所求式子计算即可.
解答 解:设$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{5}$=k,
则a=2k,b=3k,c=5k,
所以$\frac{a+b+c}{a-b+c}$=$\frac{2k+3k+5k}{2k-3k+5k}$=$\frac{10k}{4k}$=$\frac{5}{2}$.
点评 本题考查了比例的性质.解题的关键是先假设$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{5}$=k,得出a=2k,b=3k,c=5k,降低计算难度.

练习册系列答案
相关题目
10.嘉峪关市约有20.5万人,把近似数205000用科学记数法表示为( )
| A. | 205×103 | B. | 20.5×104 | C. | 2.05×105 | D. | 0.205×106 |
7.若$\frac{a}{b+c}$=$\frac{b}{c+a}$=$\frac{c}{a+b}$=k,则k的值是( )
| A. | $\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$或-1 | D. | $\frac{3}{2}$ |
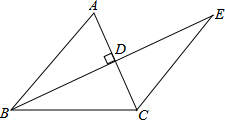 如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=56°,求∠E的度数.
如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=56°,求∠E的度数.