题目内容
15．
如图，△ABC内接于⊙O，∠OBC=42°，则∠A的度数为（ ）| A． | 84° | B． | 96° | C． | 116° | D． | 132° |
分析 连接OC，在优弧$\widehat{BC}$上取点D，连接BD、CD，根据等腰三角形的性质和三角形内角和定理求出∠BOC，根据圆周角定理求出∠BDC，根据圆内接四边形的性质计算即可．
解答 解：
连接OC，在优弧$\widehat{BC}$上取点D，连接BD、CD，
∵OB=OC，
∴∠OCB=∠OBC=42°，
∴∠BOC=96°，
∴∠BDC=$\frac{1}{2}$∠BOC=48°，
∴∠A=180°-∠BDC=132°，
故选：D．
点评 本题考查的是圆周角定理、圆内接四边形的性质，掌握圆内接四边形的对角互补是解题的关键．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
如图，DE⊥AB于E，DF⊥AC于F，若BD=CD、BE=CF，∠BAC=50°，求∠BAD=25°．
20．
如图，平面直角坐标系中，矩形ABCO与双曲线y=$\frac{k}{x}$（x＞0）交于D、E两点，将△OCD沿OD翻折，点C的对称点C′恰好落在边AB上，已知OA=3，OC=5，则AE长为（ ）
如图，平面直角坐标系中，矩形ABCO与双曲线y=$\frac{k}{x}$（x＞0）交于D、E两点，将△OCD沿OD翻折，点C的对称点C′恰好落在边AB上，已知OA=3，OC=5，则AE长为（ ）| A． | 4 | B． | 3 | C． | $\frac{26}{9}$ | D． | $\frac{25}{9}$ |
如图，点A、B、C在同一直线上，H为AC的中点，M为AB的中点，N为BC的中点，则下列说法：①MN=HC；②MH=$\frac{1}{2}$（AH-HB）；③MN=$\frac{1}{2}$（AC+HB）；④HN=$\frac{1}{2}$（HC+HB），其中正确的是（ ）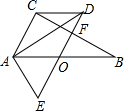
如图，已知Rt△ABC中，∠C=90°，∠B=30°，O为AB边中点，将△ABC绕点O逆时针旋转60°至△EDA位置，连接CD．