题目内容
【题目】如图,四边形![]() 内接于⊙
内接于⊙![]() ,且
,且![]() .延长
.延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.
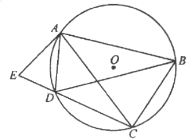
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() ,求证:
,求证:![]() 是⊙
是⊙![]() 的切线.
的切线.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据同弧所对圆周角相等可得∠ABD=∠ACD,由此可证△ABD≌△ACE,进而可得AD=AE,∠ADB=∠AEC,再由AD=AE得∠ADE=∠AEC,等量代换即可得证;
(2)由AB∥CD得∠ADE=∠BAD,结合∠ADE=∠ADB可得∠ADB=∠BAD,由此可得AB=BD,结合BD=CE,进而可证四边形ABCE为平行四边形,进而得BC∥AE,连接OA、OB、OC,再根据AB=AC,OB=OC可证AO⊥BC,结合BC∥AE即可得证.
(1)证明:由图可知:∠ABD=∠ACD,
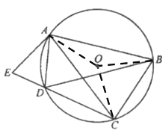
∵在△ABD与△ACE中,
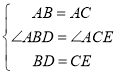
∴△ABD≌△ACE(SAS),
∴AD=AE,∠ADB=∠AEC,
∵AD=AE,
∴∠ADE=∠AEC,
∴∠ADE=∠ADB,
∴AD平分∠BDE;
(2)∵AB∥CD,
∴∠ADE=∠BAD,
∵∠ADE=∠ADB,
∴∠ADB=∠BAD,
∴AB=BD,
∵BD=CE,
∴AB=CE,
∵AB=CE,AB∥CD,
∴四边形ABCE为平行四边形,
∴BC∥AE,
如图,连接OA、OB、OC,
∵AB=AC,OB=OC
∴AO⊥BC,
又∵BC∥AE
∴AO⊥AE,
∴AE是⊙O的切线.

【题目】中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:
抽取的200名学生海选成绩分组表
组别 | 海选成绩x |
A组 | 50≤x<60 |
B组 | 60≤x<70 |
C组 | 70≤x<80 |
D组 | 80≤x<90 |
E组 | 90≤x<100 |
请根据所给信息,解答下列问题:
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 ,表示C组扇形的圆心角θ的度数为 度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?