题目内容
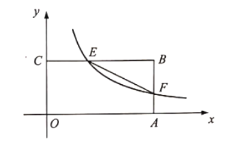
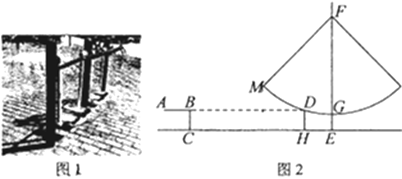
【题目】如图![]() 是某公园内健身的太空漫步机,当人踩在踏板上,握住扶手,两腿迈开到一定角度时的示意图如图
是某公园内健身的太空漫步机,当人踩在踏板上,握住扶手,两腿迈开到一定角度时的示意图如图![]() 所示,某个高
所示,某个高![]() 为
为![]() 分米的石凳旁边建一个太空漫步机,为方便行人通过,踏板与石凳之间保持了一定的距离,测得踏板静止时
分米的石凳旁边建一个太空漫步机,为方便行人通过,踏板与石凳之间保持了一定的距离,测得踏板静止时![]() 分米,
分米,![]() 分米,
分米,![]() 交
交![]() 于点
于点![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的长为_____分米;
的长为_____分米;![]() 在旋转过程中,当点
在旋转过程中,当点![]() 与点
与点![]() 的距离最小时,此时点
的距离最小时,此时点![]() 到
到![]() 的距离为_______分米.
的距离为_______分米.
【答案】![]()
![]()
【解析】
(1)连接DF,延长AD交EF于J,作GI⊥DH,根据矩形性质求出CE=BG=16分米,DG=HE,DH=GE=2.5分米,JG=0.5分米,根据勾股定理求出FG;
(2)连接BF,当M在BF上时,M离B最近,作PM⊥BC,结合(1)求出BF,BM,证所以△BPM∽△FJB,可得![]() ,即
,即![]() .
.
(1)连接DF,延长AD交EF于J,作GI⊥DH,
因为![]() 交
交![]() 于点
于点![]() ,
,![]() ,
,![]()
所以CE=BG=16分米,DG=HE,DH=GE=2.5(分米),
所以JG=2.5-2=0.5(分米)
因为![]()
所以HE=![]()
在Rt△FIJ中,设FG=x,则
由FI2=IJ2+FJ2,得
![]()
解得x=12.5(分米)
所以FG=12.5(分米)
(2)连接BF,当M在BF上时,M离B最近,作PM⊥BC,
由(1)可得
![]() (分米)
(分米)
所以BM=BF-MF=20-12.5=7.5(分米)
由BC‖EF,得∠PBM=∠BFE,
又∠BPM=∠FJB=90°
所以△BPM∽△FJB
所以![]()
即![]()
所以PM=6
故答案为:12.5,6


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目