题目内容
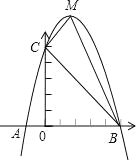
【题目】已知抛物线![]() 与坐标轴交于
与坐标轴交于![]() .
.
(1)求抛物线的解析式;
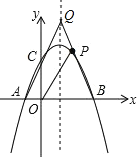
(2)设直线![]() 与该抛物线交于点
与该抛物线交于点![]() (
(![]() 在
在![]() 的左侧),记抛物线在直线
的左侧),记抛物线在直线![]() 下方的图象为
下方的图象为![]() ,在直线
,在直线![]() 下方的图象为
下方的图象为![]() ,将图象
,将图象![]() 沿直线
沿直线![]() 向下翻折得到图象
向下翻折得到图象![]() ,图象
,图象![]() 和图象
和图象![]() 两部分组成的图象记为
两部分组成的图象记为![]() .
.
①设图象![]() 的顶点为
的顶点为![]() ,当
,当![]() 落在
落在![]() 的边上时,求实数
的边上时,求实数![]() 的值.
的值.
②当![]() 时,设
时,设![]() 是图象
是图象![]() 上的动点.
上的动点.
(i)连结![]() ,过线段
,过线段![]() 的中点作
的中点作![]() 轴的平行线交
轴的平行线交![]() 轴于点
轴于点![]() ,当
,当![]() 是以
是以![]() 为直角顶点的直角角形时,直接写出
为直角顶点的直角角形时,直接写出![]() 的值.
的值.
(ii)当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,直接写出
,直接写出![]() 的最大值及相应的
的最大值及相应的![]() 的取值范围.
的取值范围.
【答案】(1)y=-x2+2x+3;(2)点Q的坐标为(1,5)或(1.-5).
【解析】
(1)点A、B、C的坐标已知,只需运用待定系数法就可求出抛物线的解析式;
(2)由四边形POP′B为菱形可得PO=PB,从而有∠POB=∠PBO.由点Q在抛物线的对称轴上可得QA=QB,从而有∠QAB=∠QBA.由△QAB与△POB相似可得∠PBO=∠QBA,从而可得点Q、P、B共线.由PO=PB可得点P在OB的垂直平分线上,从而可得xP=![]() ,代入抛物线即可求出点P的坐标,然后根据相似三角形的性质,即可得到点Q的坐标;
,代入抛物线即可求出点P的坐标,然后根据相似三角形的性质,即可得到点Q的坐标;
(1)∵A(-1,0)、B(3,0)、C(0,3)在抛物线y=ax2+bx+c上,
∴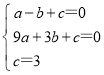 ,
,
解得 .
.
∴抛物线的解析式为y=-x2+2x+3;
(2)∵四边形POP′B为菱形,
∴PO=PB,
∴∠POB=∠PBO.
∵点Q在抛物线的对称轴上,
∴QA=QB,
∴∠QAB=∠QBA.
由△QAB与△POB相似可得∠PBO=∠QBA,
∴当Q点在x轴上方时,点Q、P、B共线.
∵PO=PB,
∴点P在OB的垂直平分线上,
∴xP=![]() ,
,
此时yP=-![]() ,
,
点P的坐标为(![]() ).
).
∵△QAB~△POB,
∴![]() ,
,
∵yP=![]() ,AB=4,OB=3,
,AB=4,OB=3,
∴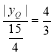 ,
,
∴|yQ|=5,
∴yQ=±5,
∵抛物线的对称轴为x=-![]() =1,
=1,
∴点Q的坐标为(1,5)或(1.-5).

 手拉手全优练考卷系列答案
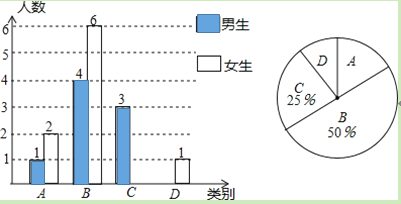
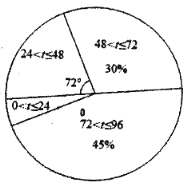
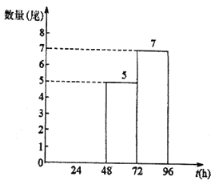
手拉手全优练考卷系列答案【题目】中华鲟是国家一级保护动物,它是大型洄游性鱼类,生在长江,长在海洋,受生态环境的影响,数量逐年下降。中华鲟研究所每年定期通过人工养殖放流来增加中华鲟的数量,每年放流的中华鲟中有少数体内安装了长效声呐标记,便于检测它们从长江到海洋的适应情况,这部分中华鲟简称为“声呐鲟”,研究所收集了它们到达下游监测点A的时间t(h)的相关数据,并制作如下不完整统计图和统计表.
已知:今年和去年分别有20尾“声呐鲟”在放流的96小时内到达监测点A,今年落在24<t≤48内的“声呐鲟”比去年多1尾,今年落在48<t≤72内的数据分别为49,60,68,68,71.
去年20尾“声呐鲟”到达监测点A 所用时间t(h)的扇形统计图
今年20尾“声呐鲟”到达监测点A所用时间t(h)的频数分布直方图
关于“声呐鲟”到达监测点A所用时间t(h)的统计表
平均数 | 中位数 | 众数 | 方差 | |
去年 | 64.2 | 68 | 73 | 715.6 |
今年 | 56.2 | a | 68 | 629.7 |
(1)请补全频数分布直方图,并根据以上信息填空:a= ;
(2)中华鲟到达海洋的时间越快,说明它从长江到海洋的适应情况就越好,请根据上述信息,选择一个统计量说明去年和今年中哪一年中华鲟从长江到海洋的适应情况更好;
(3)去年和今年该放流点共放流1300尾中华鲟,其中“声呐鲟”共有50尾,请估计今年和去年在放流72小时内共有多少尾中华鲟通过监测站A.