题目内容
12.如果函数y=x-b(b为常数)与函数y=-2x+4的图象的交点坐标是(2,0),那么关于x、y的二元一次方程组$\left\{\begin{array}{l}x-y=b\\ 2x+y=4\end{array}$的解是( )| A. | $\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=0}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-2}\\{y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=0}\\{y=-2}\end{array}\right.$ |
分析 根据函数图象交点坐标为两函数解析式组成的方程组的解进行回答.
解答 解:∵函数y=x-b(b为常数)与函数y=-2x+4的图象的交点坐标是(2,0),
∴方程组$\left\{\begin{array}{l}x-y=b\\ 2x+y=4\end{array}$的解是$\left\{\begin{array}{l}{x=2}\\{y=0}\end{array}\right.$.
故选A.
点评 本题考查了一次函数与二元一次方程(组):满足函数解析式的点就在函数的图象上,在函数的图象上的点,就一定满足函数解析式.函数图象交点坐标为两函数解析式组成的方程组的解.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
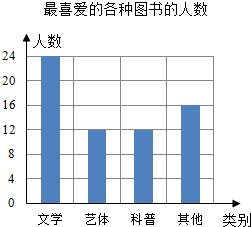 某校“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如图所示的条形统计图,则被调查的学生中喜爱文学类、艺体类、科普类的共有48人.
某校“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如图所示的条形统计图,则被调查的学生中喜爱文学类、艺体类、科普类的共有48人. 如图,平面上有射线AP和点B、点C,按下列语句要求画图:
如图,平面上有射线AP和点B、点C,按下列语句要求画图: 如图,△ABC的中线BE,CF相交于点G,P,Q分别是BG,CG的中点.
如图,△ABC的中线BE,CF相交于点G,P,Q分别是BG,CG的中点.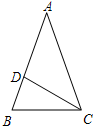 如图,在△ABC中,AB=AC,D为AB上一点,AD=CD,若∠ACD=40°,则∠B=70°.
如图,在△ABC中,AB=AC,D为AB上一点,AD=CD,若∠ACD=40°,则∠B=70°. 小红驾车从甲地到乙地,她出发第xh时距离乙地ykm,已知小红驾车中途休息了1小时,图中的折线表示她在整个驾车过程中y与x之间的函数关系.
小红驾车从甲地到乙地,她出发第xh时距离乙地ykm,已知小红驾车中途休息了1小时,图中的折线表示她在整个驾车过程中y与x之间的函数关系.