题目内容
5．已知$\sqrt{18-n}$是整数，求自然数n所有可能的值．分析 因为$\sqrt{18-n}$是整数，所以被开方数18-n是完全平方数，据此来求自然数n的值
解答 解：∵$\sqrt{18-n}$是整数，
∴18-n≥0，且18-n是完全平方数，
∴①18-n=1，即n=17；
②18-n=4，即n=14；
③18-n=9，即n=9；
④18-n=16，即n=2；
⑤18-n=0，即n=18；
综上所述，自然数n的值可以是17、14、9、2、18．
点评 考查了乘除法法则和二次根式有意义的条件．二次根式有意义的条件是被开方数是非负数．二次根式的运算法则：乘法法则$\sqrt{a}$•$\sqrt{b}$=$\sqrt{ab}$．除法法则$\sqrt{\frac{b}{a}}$=$\frac{\sqrt{b}}{\sqrt{a}}$．解题关键是分解成一个完全平方数和一个代数式的积的形式．
练习册系列答案
相关题目
13．如图是甲、乙两公司近年销售收入情况的折线统计图，根据统计图得出下列结论，其中正确的是（ ）
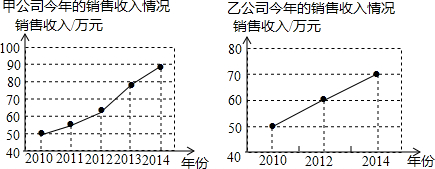
| A． | 甲公司近年的销售收入增长速度比乙公司快 | |
| B． | 乙公司近年的销售收入增长速度比甲公司快 | |
| C． | 甲、乙两公司近年的销售收入增长速度一样快 | |
| D． | 不能确定甲、乙两公司近年销售收入增长速度的快慢 |
