题目内容
17. 如图,点A的坐标为(1,0),点B在直线y=-x上,当线段AB最短时,点B的坐标为($\frac{1}{2}$,-$\frac{1}{2}$).
如图,点A的坐标为(1,0),点B在直线y=-x上,当线段AB最短时,点B的坐标为($\frac{1}{2}$,-$\frac{1}{2}$).
分析 根据线段最短,确定B点位置,解直角三角形即可.
解答  解:作AB⊥直线y=-x于点B.易知△OAB为等腰直角三角形,∠AOB=45°,OA=1.
解:作AB⊥直线y=-x于点B.易知△OAB为等腰直角三角形,∠AOB=45°,OA=1.
作BC⊥x轴于点C,可得OC=$\frac{1}{2}$OA=$\frac{1}{2}$,BC=OC=$\frac{1}{2}$.
故当线段AB最短时,点B的坐标为($\frac{1}{2}$,-$\frac{1}{2}$).
故答案为:($\frac{1}{2}$,-$\frac{1}{2}$).
点评 本题考查的是一次函数图象上点的坐标特点,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
7.为了提高天然气使用效率,保障居民的本机用气需求,某地积极推进阶梯式气价改革,若一户居民的年用气量不超过300m3,价格为2.5元/m3,若年用气量超过300m3,超出部分的价格为3 元/m3,
(1)根据题意,填写表:
(2)设一户居民的年用气量为xm3,付款金额为y元,求y关于x的解析式;
(3)若某户居民一年使用天然气所付的金额为870元,求该户居民的年用气量.
(1)根据题意,填写表:
| 一户居民的年用气量 | 150 | 250 | 350 | … |
| 付款金额/元 | 375 | 625 | 900 | … |
(3)若某户居民一年使用天然气所付的金额为870元,求该户居民的年用气量.
7.下列运算正确的是( )
| A. | 3a3+4a3=7a6 | B. | 3a2-4a2=-a2 | C. | 3a2•4a3=12a3 | D. | (3a3)2÷4a3=$\frac{3}{4}$a2 |




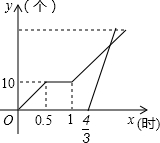 某车间甲、乙两名工人加工相同数量的相同零件,甲因特殊原因中间休息一段时间,重新开始工作后按原来的工作效率继续加工,乙因迟到,为了尽快完成任务,以甲3倍的工作效率加工,直到任务结束.如图是他们分别加工零件的数量y(个)与工作时间x(时)的函数图象
某车间甲、乙两名工人加工相同数量的相同零件,甲因特殊原因中间休息一段时间,重新开始工作后按原来的工作效率继续加工,乙因迟到,为了尽快完成任务,以甲3倍的工作效率加工,直到任务结束.如图是他们分别加工零件的数量y(个)与工作时间x(时)的函数图象 顺达旅行社为吸引游客到黄山景区旅游,推出如下收费标准:
顺达旅行社为吸引游客到黄山景区旅游,推出如下收费标准: