题目内容
6. ①已知(3m-2)2+|n+4|=0,先化简再求值:2m-{n+[4m-3(m+2n)+6m]-5n}
①已知(3m-2)2+|n+4|=0,先化简再求值:2m-{n+[4m-3(m+2n)+6m]-5n}②有理数a,b,c在数轴上的位置如图所示,化简:|a+c|-|a-b-c|-|b-c|+|b+c|.
分析 ①根据非负性即可求出m与n的值,然后化简求值即可;②根据数轴比较a+c、a-b-c、b-c、b+c与0的大小,然后进行化简运算即可.
解答 解:①根据非负性得:m=1.5,n=-4,
原式=2m-(n+4m-3m-6n+6m-5n)
=2m-(-10n+7m)
=-5m+10n
=-32.5;
②由数轴可知:c<b<0<a,
∴a+c<0,a-b-c>0,b-c>0,b+c<0,
原式=-a-c-(a-b-c)-(b-c)-(b+c)
=-a-c-a+b+c-b+c-b-c
=-2a-b;
点评 本题考查整式的化简,涉及非负数的性质,利用数轴比较数的大小,代入求值等知识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.下列命题中,假命题是( )
| A. | 两条边相等的两个直角三角形全等 | |
| B. | 等腰三角形顶角的平分线把它分成两个全等三角形 | |
| C. | 有一个角是60°的等腰三角形是等边三角形 | |
| D. | 底边相等的两个等腰直角三角形全等. |
 小华和小红都从同一点O出发,当小华向正北走了80米到A点,小红向正东走到B点时,两人相距为170米,则小红向正东方向走了多少米?
小华和小红都从同一点O出发,当小华向正北走了80米到A点,小红向正东走到B点时,两人相距为170米,则小红向正东方向走了多少米?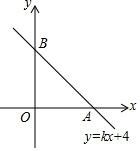 如图,在直角坐标系中,直线y=kx+4与x轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求
如图,在直角坐标系中,直线y=kx+4与x轴正半轴交于一点A,与y轴交于点B,已知△OAB的面积为10,求