Question

如图，△ABC的边AB=3，AC=2，Ⅰ、Ⅱ、Ⅲ分别表示以AB、AC、BC为边的正方形，求图中三个阴影部分的面积之和的最大值是多少？

Answer 1

分析：把△CFH绕点C顺时针旋转90°，使CF与BC重合，H旋转到H'的位置，根据旋转的性质和正方形的性质有A、C、H'在一直线上，且BC为△ABH'的中线，得到S_△CHF=S_△BCH'=S_△ABC，同理：S_△BDG=S_△AEM=S_△ABC，所以S_{阴影部分面积}=3S_△ABC=3×

1

2

AB×AC×sin∠BAC，即当AB⊥AC时，S_△ABC最大值为：

1

2

×2×3=3，即可得到三个阴影部分的面积之和的最大值．

解答：解：把△CFH绕点C顺时针旋转90°，使CF与BC重合，H旋转到H'的位置，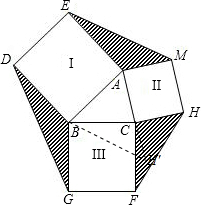
∵四边形ACHM为正方形，∠ACH=90°，CA=CH=CH′，
∴A、C、H'在一直线上，且BC为△ABH'的中线，
∴S_△CHF=S_△BCH'=S_△ABC，
同理：S_△BDG=S_△AEM=S_△ABC，
所以阴影部分面积之和为S_△ABC的3倍，
又AB=3，AC=2，
∴S_{阴影部分面积}=3S_△ABC=3×

1

2

AB×AC×sin∠BAC，
当∠BAC最大时阴影部分面积之和最大，
即当AB⊥AC时，S_△ABC最大值为：

1

2

×2×3=3
∴阴影部分面积的最大值为3×3=9（平方单位）．

点评：本题考查了旋转的性质：旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等．也考查了正方形的性质和三角形的面积公式．