Question

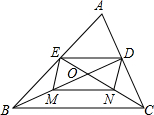如图，△ABC的边AC、AB上的中线BD、CE相交于点O，M、N分别是BO、CO的中点，顺次连接点D、E、M、N．
（1）求证：四边形DEMN是平行四边形；
（2）当△ABC满足什么条件时，四边形DEMN是矩形，请说明理由．

Answer 1

分析：（1）由中位线定理，可得ED∥BC，MN∥BC，且都等于边长BC的一半．分析到此，此题便可解答．
（2）连接OA，则AO∥ME∥DN；若△ABC为等腰三角形时，则OA和BC垂直，进而求出即可．

解答：证明：（1）△ABC的边AC、AB上的中线BD、CE相交于点O，M、N分别是BO、CO的中点，
∴ED∥BC且ED=

1

2

BC，
MN∥BC且MN=

1

2

BC，
∴ED∥MN且ED=MN，
∴四边形MNDE是平行四边形．

（2）连接OA并延长交BC于点F；
∵E，M分别是AB，BO中点，
∴AO∥ME∥DN，
当△ABC为等腰三角形时，
∴AO⊥BC，
∵四边形DEMN是平行四边形，
∴EM⊥MN；
∴此时四边形DEMN是矩形．

点评：本题考查了平行四边形的判定和三角形的中位线定理，三角形的中位线的性质定理，为证明线段相等和平行提供了依据．