题目内容
6．已知直线y=x+3与x轴交于点B，它与反比例函数y=$\frac{4}{x}$的图象在第一象限内交于点A，直线l经过点A，且与x轴交于点C，若△ABC的面积为6，求直线l的解析式．分析 由直线y=x+3与x轴交于点B，求得B（-3，0），由于直线y=x+3与反比例函数y=$\frac{4}{x}$的图象在第一象限内交于点A，求得A（1，4），设点C的坐标为（a，0），根据面积公式列方程得到a=0，于是得到C（0，0），设直线l的解析式为：y=kx，把A（1，4）代入即可得到结论．
解答 解：∵直线y=x+3与x轴交于点B，
∴B（-3，0），
∵直线y=x+3与反比例函数y=$\frac{4}{x}$的图象在第一象限内交于点A，
解$\left\{\begin{array}{l}{y=x+3}\\{y=\frac{4}{x}}\end{array}\right.$，得$\left\{\begin{array}{l}{x=-4}\\{y=-1}\end{array}\right.$，或$\left\{\begin{array}{l}{x=1}\\{y=4}\end{array}\right.$，
∴A（1，4），
设点C的坐标为（a，0），
∴S△ABC=$\frac{1}{2}$（a+3）×4=6，
∴a=0，
∴C（0，0），
设直线l的解析式为：y=kx，
把A（1，4）代入得：4=k，
∴直线l的解析式为：y=4x．
点评 此题主要考查了反比例函数与一次函数的交点问题，解方程组，待定系数法求函数的解析式，弄清题意和数量关系是解题的关键．
练习册系列答案
名校课堂系列答案
相关题目
如图，a、b为数轴上不同两点．则：
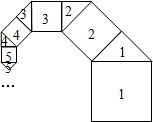如图所示，第1个正方形的边是第1个等腰直角三角形的斜边，第1个等腰直角三角形的直角边是第2个正方形的边，第2个正方形的边是第2个等腰三角形的斜边…依此不断连接下去，设第1个正方形的边长为2，求：
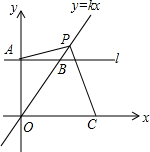如图，直线l∥x轴，交y轴于点A（0，2），交直线y=kx于点B，P是线段OB延长线上一点，连接AP作PC⊥AP交x轴于点C，连接AC交OB于D，E是直线CP与y轴的交点．如果∠ACE=∠AEC，$\frac{PD}{OD}$=2，求$\frac{PA}{PC}$的值．
如图，在平面直角坐标系中，四边形OABC是平行四边形，O（0，0），A（1，-2），B（3，1），反比例函数y=$\frac{k}{x}$（k≠0）的图象经过点C．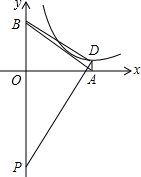
如图，在平面直角坐标系中，直线y=-$\frac{3}{4}$x+6与x轴、y轴的正半轴分别相交于点A，B两点，点D在反比例函数y=$\frac{k}{x}$（k＞0）的图象上，DA⊥OA，点P在y轴负半轴上，OP=14．
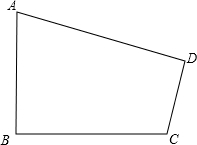威海刘公岛是全国知名的旅游景区之一，该岛的近似形状如图所示．经地质人员测量得知：AB=4km，CD=2km，∠A=60°，∠B=∠D=90°．利用这些条件你能求出该岛的面积吗？