题目内容
如图,已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
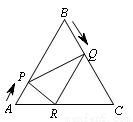
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR//BA交AC于点R,连结PR,当t为何值时,△APR∽△PRQ?
(1)△BPQ是等边三角形;(2)S=-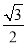 t2+3
t2+3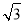 t;(3)当t=
t;(3)当t=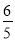 时,△APR∽△PRQ.
时,△APR∽△PRQ.
【解析】
试题分析:(1)当t=2时,可分别计算出BP、BQ的长,再对△BPQ的形状进行判断;
(2)∠B为60°特殊角,过Q作QE⊥AB,垂足为E,则BQ、BP、高EQ的长可用t表示,S与t的函数关系式也可求;
(3)由题目线段的长度可证得△CRQ为等边三角形,进而得出四边形EPRQ是矩形,由△APR∽△PRQ,可得出∠QPR=60°,利用60°的特殊角列出一方程即可求得t的值.
试题解析:(1)△BPQ是等边三角形
当t=2时
AP=2×1=2,BQ=2×2=4
∴BP=AB-AP=6-2=4
∴BQ=BP
又∵∠B=60°
∴△BPQ是等边三角形;
(2)过Q作QE⊥AB,垂足为E
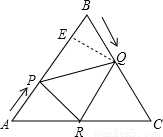
由QB=2t,得QE=2t•sin60°=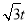
由AP=t,得PB=6-t
∴S△BPQ=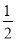 ×BP×QE=
×BP×QE=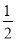 (6-t)×
(6-t)×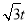 =-
=-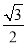 t2+3
t2+3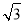 t
t
∴S=-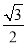 t2+3
t2+3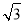 t
t
(3)∵QR∥BA
∴∠QRC=∠A=60°,∠RQC=∠B=60°
∴△QRC是等边三角形
∴QR=RC=QC=6-2t
∵BE=BQ•cos60°=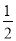 ×2t=t
×2t=t
∴EP=AB-AP-BE=6-t-t=6-2t
∴EP∥QR,EP=QR
∴四边形EPRQ是平行四边形
∴PR=EQ=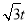
又∵∠PEQ=90°,
∴∠APR=∠PRQ=90°
∵△APR∽△PRQ,
∴∠QPR=∠A=60°
∴tan60°=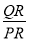
即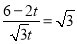
解得t=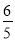
∴当t=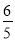 时,△APR∽△PRQ.
时,△APR∽△PRQ.
考点:1.相似三角形的性质;2.等边三角形的性质;3.平行四边形的性质;4.解直角三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
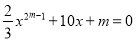 是关于
是关于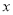 的一元二次方程,则m的值应为( )
的一元二次方程,则m的值应为( )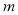 =2 B.
=2 B.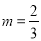 C.
C.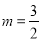 D.无法确定
D.无法确定
 是反比例函数,则a=____
是反比例函数,则a=____