题目内容
已知⊙O内切于扇形OAB,∠AOB=60°,求扇形
的长与⊙O的周长之比.
 |
| AB |
考点:切线的性质,弧长的计算
专题:
分析:利用弧长公式可求得弧AB的长,然后再利用圆相切求得小圆与大圆的半径关系,利用周长公式求比值.
解答: 解:如图,连接O′F,OO′,并延长OO′,
解:如图,连接O′F,OO′,并延长OO′,
因为⊙O和⊙O′相切,
所以OO′经过点C,
又因为OB与⊙O′相切于F,
所以O′F⊥OB.
因为∠AOB=60°,
所以∠BOC=30°,
所以O′F=
OO′.
设⊙O′的半径为r,
所以r=
OO′=
(R-r),
所以R=3r,
所以
的长与内切圆⊙O'的周长的比=1:2.
 解:如图,连接O′F,OO′,并延长OO′,
解:如图,连接O′F,OO′,并延长OO′,因为⊙O和⊙O′相切,
所以OO′经过点C,
又因为OB与⊙O′相切于F,
所以O′F⊥OB.
因为∠AOB=60°,
所以∠BOC=30°,
所以O′F=
| 1 |
| 2 |
设⊙O′的半径为r,
所以r=
| 1 |
| 2 |
| 1 |
| 2 |
所以R=3r,
所以
 |
| AB |
点评:本题主要考查了切线性质和弧长公式,难度适中.

练习册系列答案
相关题目
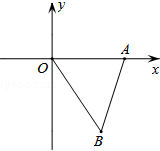 如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,-3),△EFD是△ABO关于原点O的位似图形,且原图形与它位似比为2,则点F的坐标为
如图,平面直角坐标系xOy中,点A、B的坐标分别为(3,0)、(2,-3),△EFD是△ABO关于原点O的位似图形,且原图形与它位似比为2,则点F的坐标为