题目内容
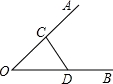
如图,BD是∠ABC的平分线,DE∥CB,交AB于点E,∠A=45°,∠BDC=60°,求△BDE各内角的度数.

【考点】三角形内角和定理;平行线的性质.
【专题】计算题.
【分析】利用三角形的外角性质,先求∠ABD,再根据角平分线的定义,可得∠DBC=∠ABD,运用平行线的性质得∠BDE的度数,根据三角形内角和定理可求∠BED的度数.
【解答】解:∵∠A=45°,∠BDC=60°,
∴∠ABD=∠BDC﹣∠A=15°.
∵BD是∠ABC的角平分线,
∴∠DBC=∠EBD=15°,
∵DE∥BC,
∴∠BDE=∠DBC=15°;
∴∠BED=180°﹣∠EBD﹣∠EDB=150°.
【点评】本题综合考查了平行线的性质及三角形内角与外角的关系,三角形内角和定理.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目



 ﹣2)2015•(
﹣2)2015•(
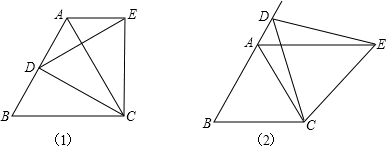
 长方形按如图所示的方式折叠,若∠AEB′=30°,则∠B′EF=( )
长方形按如图所示的方式折叠,若∠AEB′=30°,则∠B′EF=( )