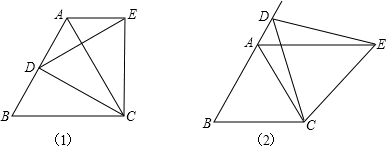
题目内容
如图(1),等边△ABC中,D是AB边上的动点,以CD为一边,向上作等边△EDC,连接AE.
(1)求证:AE∥BC;
(2)如图(2),将(1)中的动点D运动到边BA的延长线上,仍作等边△EDC,请问是否仍有AE∥BC?证明你的猜想.
【考点】全等三角形的判定与性质;等边三角形的性质.
【分析】(1)证明△ACE≌△BCD推出∠ACB=∠EAC即可证.
(2)证明△DBC≌△EAC可推出∠EAC=∠ACB,由此可证.
【解答】解:(1)证明:∵∠ACB=60°,∠DCE=60°,
∴∠BCD=60°﹣∠ACD,∠ACE=60°﹣∠ACD,
∴∠BCD=∠ACE,
在△DBC和△EAC中,
∵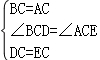 ,
,
∴△DBC≌△EAC(SAS),
∴∠EAC=∠B=60°.
又∵∠ACB=60°
∴∠EAC=∠ACB
∴AE∥BC.
(2)结论:AE∥BC,
理由:∵△ABC、△EDC为等边三角形
∴BC=AC,DC=CE,∠BCA=∠DCE=60°
∠BCA+∠ACD=∠DCE+∠ACD,
即∠BCD=∠ACE,
在△DBC和△EAC中,
∵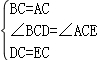 ,
,
∴△DBC≌△EAC(SAS),
∴∠EAC=∠B=60°,
又∵∠ACB=60°
∴∠EAC=∠ACB
∴AE∥BC.
【点评】本题考查的是全等三角形的判定和性质.关键是证明△ACE≌△BCD.

练习册系列答案
相关题目



 |=2 B.
|=2 B. =±7 C.
=±7 C. =﹣5 D.
=﹣5 D. =﹣
=﹣
 有意义,则x应满足__________.
有意义,则x应满足__________.