题目内容
如图，将一张长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，ED′的延长线与BC相交于点G，若∠EFG=62°，则∠1=考点：平行线的性质,翻折变换（折叠问题）
专题：
分析：由矩形的对边平行可得∠DEF=∠EFG，∠1=∠DEG，由折叠可得∠GEF=∠DEF，那么所求的∠1=2∠EFG．
解答：解：∵四边形ABCD是矩形，
∴AD∥BC，
∴∠DEF=∠EFG，∠1=∠DEG．
∵∠DEF=∠GEF，∠EFG=62°，
∴∠1=2∠EFG=124°．
故答案为：124°．
∴AD∥BC，
∴∠DEF=∠EFG，∠1=∠DEG．
∵∠DEF=∠GEF，∠EFG=62°，
∴∠1=2∠EFG=124°．
故答案为：124°．
点评：此题主要考查了翻折变换和平行线的性质，解决本题的关键是根据折叠及矩形性质把所求角整理为和所给角的度数有关的角．
练习册系列答案
相关题目
科学家为了探测火星上是否有智能生物人，有人建议向火星发射如下3×3的九宫方格数据图，图中数据满足各行、各列及对角线上三个数之和都相等，如果火星上有智能生物人，那么他们就可以从这种“数学语言”了解到地球上也有智能生物人．如图是某研究员在3×3九宫方格内设计的一个准备向火星发射的图案的一部分，格内填写了一些式子和数．
如图，已知∠MON=30°，P为∠MON内一定点，点A为OM上的点，B为ON上的点，当△PAB的周长取最小值时，则∠APB度数是
正方形A1B1C1O，A2B2C2C1，A3B3C3C2，…按如图所示的方式放置，点A1，A2，A3和点C1，C2，C3，…分别在直线y=kx+b（k＞0）和x轴上，已知点B1（1，1），B2（3，2），则B2014的坐标是
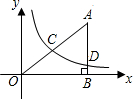在直角坐标系中，有如图所示的Rt△ABO，AB⊥x轴于点B，斜边AO=10，sin∠AOB=| 3 |
| 5 |
| k |
| x |
A、（8，
| ||
B、（6，
| ||
C、（
| ||
D、（8，
|