题目内容
设方程组
有实数解,求a+b的值.
|
考点:高次方程
专题:
分析:根据方程的结构特点,将所给的三个方程相加得:(a+b+1)(x2+x+1)=0;根据题意,讨论a+b+1是否为0,即可解决问题.
解答:解:
,
将上述三个方程相加得:(a+b+1)(x2+x+1)=0,
若a+b+1≠0,则x2+x+1=0,
∵△=12-4×1×1<0,
∴该方程无解,这与已知矛盾,
∴a+b+1=0,a+b=-1.
|
将上述三个方程相加得:(a+b+1)(x2+x+1)=0,
若a+b+1≠0,则x2+x+1=0,
∵△=12-4×1×1<0,
∴该方程无解,这与已知矛盾,
∴a+b+1=0,a+b=-1.
点评:该题主要考查了一元二次方程根的判别式及其应用问题;解题的关键是深入观察探究方程的结构特点,灵活选用解题方法,大胆猜测推理、科学论证解答.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
近些年,中国城市中产阶级规模快速扩大,2012年增至413 000 000人,用科学记数法表示为( )人.
| A、413×106 |
| B、4.13×108 |
| C、4.13×106 |
| D、0.413×109 |
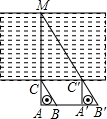 如图,一名同学拿一把含30°角直角三角尺ABC(即∠ACB=30°)目测一条河的宽度,他先在岸边点A处顺着30°角的邻边AC的方向看见河对岸的一棵树M,然后沿30°角的对边AB的方向前进到B′处,顺着斜边B′C′的方向看见树M,并测得AA′=100米,则他目测的河宽MC大约是多少米(精确到1米)?
如图,一名同学拿一把含30°角直角三角尺ABC(即∠ACB=30°)目测一条河的宽度,他先在岸边点A处顺着30°角的邻边AC的方向看见河对岸的一棵树M,然后沿30°角的对边AB的方向前进到B′处,顺着斜边B′C′的方向看见树M,并测得AA′=100米,则他目测的河宽MC大约是多少米(精确到1米)?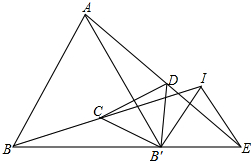 如图,已知△ABB′与△IB′E是等边三角形,连接AE、BI,C、D分别为BI、AE的中点,求证:△CDB′是等边三角形.
如图,已知△ABB′与△IB′E是等边三角形,连接AE、BI,C、D分别为BI、AE的中点,求证:△CDB′是等边三角形. 如图所示,已知点O是AB中点,且AP=28cm,点P是AB上一点,点AP:PB=5:2,则OP=
如图所示,已知点O是AB中点,且AP=28cm,点P是AB上一点,点AP:PB=5:2,则OP= 如图,在梯形ABCD中,AD∥BC,AE平分∠BAD,BE平分∠ABC,且AE、BE交CD于点E.试说明AD=AB-BC的理由.
如图,在梯形ABCD中,AD∥BC,AE平分∠BAD,BE平分∠ABC,且AE、BE交CD于点E.试说明AD=AB-BC的理由. 如图,周长为24的五边形ABCDE,被对角线BE分为等腰三角形ABE及矩形BCDE,且AB=BC.设AB长为x,CD为y,求y与x之间的函数关系,写出自变量的取值范围.
如图,周长为24的五边形ABCDE,被对角线BE分为等腰三角形ABE及矩形BCDE,且AB=BC.设AB长为x,CD为y,求y与x之间的函数关系,写出自变量的取值范围.