题目内容
关于x的一元二次方程kx2-2(k+4)x+2(k2-2)=0的两根都为正数,求k的取值范围.
考点:一元二次方程根的分布
专题:计算题,代数综合题,分类讨论
分析:分类讨论,①k>0,②k<0,只要满足抛物线y=kx2-2(k+4)x+2(k2-2)与x轴的交点在x轴的正半轴即可;
解答:解:抛物线y=kx2-2(k+4)x+2(k2-2)的对称轴为直线x=
,
①若k>0,如图所示:

此时当x=0时,y>0,对称轴在y轴的右侧,
即可得
,
解得:k>
;
②若k<0,如图所示:

此时当x=0时,y<0,对称轴在y轴右侧,
即可得
,
解得:-4<k<-
.
综上可得:k的取值范围是k>
或-4<k<-
.
| 2(k+4) |
| 2k |
①若k>0,如图所示:

此时当x=0时,y>0,对称轴在y轴的右侧,
即可得
|
解得:k>
| 2 |
②若k<0,如图所示:

此时当x=0时,y<0,对称轴在y轴右侧,
即可得
|
解得:-4<k<-
| 2 |
综上可得:k的取值范围是k>
| 2 |
| 2 |
点评:此题考查了一元二次方程根的分布,关键是利用抛物线与y轴、对称轴与x轴的交点情况进行限制,难度较大,注意理解此类题目的解题方法.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
若抛物线y=0.5x2+3x+m与x轴没有交点,则m的取值范围是( )
| A、m≤4.5 |
| B、m≥4.5 |
| C、m>4.5 |
| D、以上都不对 |
 如图,直线MN与x轴,y轴正半轴分别交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,已知AC=10,OA=8.
如图,直线MN与x轴,y轴正半轴分别交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,已知AC=10,OA=8.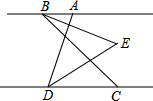 如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求:
如图,已知AB∥CD,BE平分∠ABC,DE平分∠ADC,∠BAD=80°,试求: 如图:已知长方体的高为h,底面是边长a的正方形.
如图:已知长方体的高为h,底面是边长a的正方形.