题目内容
15．
如图，OB是∠AOC的平分线，OD是∠COE的平分线，若∠AOC=70°，∠COE=40°，那么∠BOD等于（ ）| A． | 50° | B． | 55° | C． | 60° | D． | 65° |
分析 利用角平分线的性质和角与角的和差关系计算即可．
解答 解：∵OB是∠AOC的平分线，OD是∠COE的平分线
∴∠COD=$\frac{1}{2}$∠COE，∠BOC=$\frac{1}{2}$∠AOC
又∵∠AOC=70°，∠COE=40°
∴∠COD=20°，∠BOC=35°，
那么∠BOD=∠COD+∠BOC=20°+35°=55°
∠BOD=55°．
故选B．
点评 本题考查角与角之间的运算和角平分线的知识点，注意结合图形，发现角与角之间的关系，进而求解．
练习册系列答案
发散思维新课堂系列答案
相关题目
5．
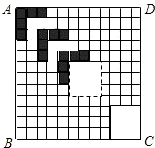如图，正方形ABCD的边长为12，划分成12×12个小正方形格．将边长为n（n为整数，且2≤n≤11）的黑白两色正方形纸片按图中的方式黑白相间地摆放，第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格，第二张纸片盖住第一张纸片的部分恰好为（n-1）×（n-1）的正方形．如此摆放下去，最后直到纸片盖住正方形ABCD的右下角为止．
请你认真观察思考后回答下列问题：
（1）由于正方形纸片边长n的取值不同，完成摆放时所使用正方形纸片的张数也不同，请填写下表：
（2）设正方形ABCD被纸片盖住的面积（重合部分只计一次）为S1，未被盖住的面积为S2．
①当n=2时，求S1：S2的值；
②用含n的代数式表示S2．
如图，正方形ABCD的边长为12，划分成12×12个小正方形格．将边长为n（n为整数，且2≤n≤11）的黑白两色正方形纸片按图中的方式黑白相间地摆放，第一张n×n的纸片正好盖住正方形ABCD左上角的n×n个小正方形格，第二张纸片盖住第一张纸片的部分恰好为（n-1）×（n-1）的正方形．如此摆放下去，最后直到纸片盖住正方形ABCD的右下角为止．请你认真观察思考后回答下列问题：
（1）由于正方形纸片边长n的取值不同，完成摆放时所使用正方形纸片的张数也不同，请填写下表：
| 纸片的边长n | 2 | 3 | 4 | 5 | 6 |
| 使用的纸片张数 | 11 | 10 | 9 | 8 | 7 |
①当n=2时，求S1：S2的值；
②用含n的代数式表示S2．
6．
有理数a、b在数轴上的位置如图所示，下列结论中正确的是（ ）
有理数a、b在数轴上的位置如图所示，下列结论中正确的是（ ）| A． | a＜b | B． | ab＞0 | C． | a+b＜0 | D． | a-b＜0 |
10．当a=-$\frac{1}{2}$，b=4时，多项式2a2b-3a-3a2b+2a的值为（ ）
| A． | 2 | B． | -2 | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |