题目内容
20.已知直角三角形斜边长为10cm,周长为22cm,则此直角三角形的面积为11cm2.分析 设一条直角边为xcm,另一条直角边bcm,再根据勾股定理求出2ab的值,根据三角形的面积公式即可得出结论.
解答 解:∵直角三角形斜边长为10cm,周长为22cm,
∴设一条直角边为acm,另一条直角边为bcm,
∴a+b=22-10=12(cm),a2+b2=102=100,
∴(a+b)2=a2+b2+2ab=12×12=144,
∴2ab=144-(a2+b2)=144-100=44,
∴$\frac{1}{2}$ab=11.
∴此三角形的面积为11cm2.
故答案为:11cm2.
点评 本题考查的是勾股定理、三角形面积的计算方法;熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
11.抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x,纵坐标y的对应值如表:
从上表可知,下列说法错误的是( )
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | -$\frac{3}{2}$ | 1 | $\frac{5}{2}$ | 3 | $\frac{5}{2}$ | 1 | … |
| A. | 对称轴为直线x=2 | B. | 图象开口向下 | C. | 顶点坐标(2,3) | D. | 当x=5时,y=$\frac{3}{2}$ |
15.小芳有两根长度为4cm和9cm的木条,她想钉一个三角形木框,桌上有下列长度的几根木条,她应该选择长度为( )的木条.
| A. | 5cm | B. | 3cm | C. | 12cm | D. | 17cm |
10. 如图,在菱形ABCD中,O为AC和BD交点,则∠COD等于( )
如图,在菱形ABCD中,O为AC和BD交点,则∠COD等于( )
 如图,在菱形ABCD中,O为AC和BD交点,则∠COD等于( )
如图,在菱形ABCD中,O为AC和BD交点,则∠COD等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
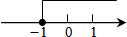
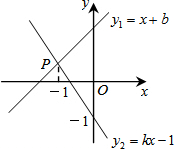 如图,已知直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b≤kx-1的解集在数轴上表示正确的是( )
如图,已知直线y1=x+b与y2=kx-1相交于点P,点P的横坐标为-1,则关于x的不等式x+b≤kx-1的解集在数轴上表示正确的是( )
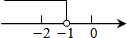
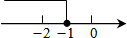
 有理数a、b、c在数轴上的位置如图所示,试化简:|c-b|-|a-b|+|c|.
有理数a、b、c在数轴上的位置如图所示,试化简:|c-b|-|a-b|+|c|.