题目内容
 如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB=
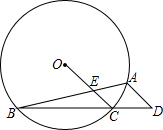
如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB= ,抛物线y=ax2+bx经过点A(4,0)与点(2,6).
,抛物线y=ax2+bx经过点A(4,0)与点(2,6).
(1)求抛物线的函数解析式;
(2)直线m与⊙C相切于点A,交y轴于点D.求证:AD∥OB;
(3)动点P在线段OB上,从点O出发向点B运动;同时动点Q在线段DA上,从点D出发向点A运动;点P的速度为每秒一个单位长,点Q的速度为每秒2个单位长,当PQ⊥AD时,求运动时间t的值.
解:(1)∵抛物线y=ax2+bx经过点A(4,0)与点(-2,6),
∴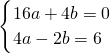 ,
,
解得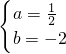 ,
,
∴抛物线的解析式为:y= x2-2x;
x2-2x;
(2)如图,连接AC交OB于点E,连接OC、OB,
∵OC=OB,AB=AO,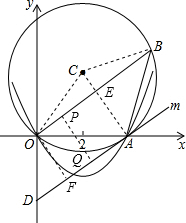
∴AC⊥OB,
∵AD为切线,
∴AC⊥AD,
∴AD∥OB;
(3)∵tan∠AOB= ,
,
∴sin∠AOB= ,
,
∴AE=OA•sin∠AOB=4× =2.4,
=2.4,
∵AD∥OB,
∴∠OAD=∠AOB,
∴OD=OA•tan∠OAD=OA•tan∠AOB=4× =3,
=3,
当PQ⊥AD时,OP=t,DQ=2t,
过O点作OF⊥AD于F,
在Rt△ODF中,OD=3,OF=AE=2.4,DF=DQ-FQ=DQ-OP=2t-t=t,
由勾股定理得:DF= =
= =1.8,
=1.8,
∴t=1.8秒.
分析:(1)把经过的点的坐标代入抛物线表达式,然后利用待定系数法求二次函数解析式;
(2)连接AC交OB于点E,连接OC、OB,然后根据到线段两端点距离相等的点在线段的垂直平分线上求出AC⊥OB,再根据圆的切线的定义求出AC⊥AD,然后根据垂直于同一直线的两直线互相平行证明;
(3)根据∠AOB的正切值求出余弦值,然后求出AE,再利用∠OAD的正切值求出OD的长,表示出OP、OQ,再过O点作OF⊥AD于F,用t表示出DF,在Rt△ODF中,利用勾股定理列式求出DF,从而得解.
点评:本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,到线段两端点距离相等的点在线段垂直平分线上,圆的切线的定义,解直角三角形,勾股定理的应用,平行线间的距离相等的性质,难度较大,作辅助线构造出直角三角形是解题的关键.
∴
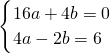 ,
,解得
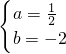 ,
,∴抛物线的解析式为:y=
 x2-2x;
x2-2x;(2)如图,连接AC交OB于点E,连接OC、OB,
∵OC=OB,AB=AO,

∴AC⊥OB,
∵AD为切线,
∴AC⊥AD,
∴AD∥OB;
(3)∵tan∠AOB=
 ,
,∴sin∠AOB=
 ,
,∴AE=OA•sin∠AOB=4×
 =2.4,
=2.4,∵AD∥OB,
∴∠OAD=∠AOB,
∴OD=OA•tan∠OAD=OA•tan∠AOB=4×
 =3,
=3,当PQ⊥AD时,OP=t,DQ=2t,
过O点作OF⊥AD于F,
在Rt△ODF中,OD=3,OF=AE=2.4,DF=DQ-FQ=DQ-OP=2t-t=t,
由勾股定理得:DF=
 =
= =1.8,
=1.8,∴t=1.8秒.
分析:(1)把经过的点的坐标代入抛物线表达式,然后利用待定系数法求二次函数解析式;
(2)连接AC交OB于点E,连接OC、OB,然后根据到线段两端点距离相等的点在线段的垂直平分线上求出AC⊥OB,再根据圆的切线的定义求出AC⊥AD,然后根据垂直于同一直线的两直线互相平行证明;
(3)根据∠AOB的正切值求出余弦值,然后求出AE,再利用∠OAD的正切值求出OD的长,表示出OP、OQ,再过O点作OF⊥AD于F,用t表示出DF,在Rt△ODF中,利用勾股定理列式求出DF,从而得解.
点评:本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,到线段两端点距离相等的点在线段垂直平分线上,圆的切线的定义,解直角三角形,勾股定理的应用,平行线间的距离相等的性质,难度较大,作辅助线构造出直角三角形是解题的关键.

练习册系列答案
相关题目
 如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④
如图,⊙O的内接△ABC的外角∠ACE的平分线交⊙O于点D.DF⊥AC,垂足为F,DE⊥BC,垂足为E.给出下列4个结论:①CE=CF;②∠ACB=∠EDF;③DE是⊙O的切线;④ |
| AD |
 |
| BD |
| A、①②③ | B、②③④ |
| C、①③④ | D、①②④ |
 如图,⊙O的内接多边形周长为3,⊙O的外切多边形周长为3.4,则下列各数中与此圆的周长最接近的是( )
如图,⊙O的内接多边形周长为3,⊙O的外切多边形周长为3.4,则下列各数中与此圆的周长最接近的是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 OC交AB于E.
OC交AB于E. 如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB=
如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB= 如图,⊙O的内接四边形ABCD中,AB=AD,∠BAD=30°,AC=4,求四边形ABCD的面积.
如图,⊙O的内接四边形ABCD中,AB=AD,∠BAD=30°,AC=4,求四边形ABCD的面积.