题目内容
分解因式:
(1)a3-6a2+9a;
(2)(x2+x)2-(x+1)2.
(1)a3-6a2+9a;
(2)(x2+x)2-(x+1)2.
考点:提公因式法与公式法的综合运用
专题:
分析:(1)首先提公因式a,然后利用完全平方公式分解;
(2)利用提供式分解,然后利用平方差公式即可分解.
(2)利用提供式分解,然后利用平方差公式即可分解.
解答:解:(1)原式=a(a2-6a+9)
=a(a-3)2;
(2)原式=x2(x+1)2-(x+1)2
=(x+1)2(x2-1)
=(x+1)3(x-1).
=a(a-3)2;
(2)原式=x2(x+1)2-(x+1)2
=(x+1)2(x2-1)
=(x+1)3(x-1).
点评:本题考查了提公因式法,公式法分解因式,提取公因式后利用完全平方公式进行二次分解,注意分解要彻底.

练习册系列答案
相关题目
若a,b互为相反数,c,d互为倒数,m的绝对值等于1,则-(a+b)-cd-m的值为( )
| A、0 | B、-2 |
| C、0或-2 | D、任意有理数 |
 如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.
如图,∠1=∠ACB,∠2=∠3,FH⊥AB于H,求证:CD⊥AB.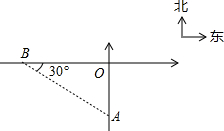 如图,钓鱼岛A在我某雷达站B东偏南30°方向400公里处,我歼10飞机在钓鱼岛A处巡逻时,被告知,某未通告飞行物从雷达站正东方飞来,0.2小时后即将达到我防空识别区边缘点O.已知∠AOB=90°,问我歼10飞机至少应以什么速度飞行才可以在其刚进入我识别区时予以识别?
如图,钓鱼岛A在我某雷达站B东偏南30°方向400公里处,我歼10飞机在钓鱼岛A处巡逻时,被告知,某未通告飞行物从雷达站正东方飞来,0.2小时后即将达到我防空识别区边缘点O.已知∠AOB=90°,问我歼10飞机至少应以什么速度飞行才可以在其刚进入我识别区时予以识别?