题目内容
5.解方程:(1)4(x+2)2-25=0;
(2)$\frac{1}{2}$(x-3)3=32.
分析 (1)方程变形后,利用平方根定义开方即可求出解;
(2)方程变形后,利用立方根定义开立方即可求出解.
解答 解:(1)方程变形得:(x+2)2=$\frac{25}{4}$,
开方得:x+2=±$\frac{5}{2}$,
解得:x1=$\frac{1}{2}$,x2=-$\frac{9}{2}$;
(2)方程整理得:(x-3)3=64,
开立方得:x-3=4,
解得:x=7.
点评 此题考查了立方根,以及平方根,熟练掌握各自的定义是解本题的关键.

练习册系列答案
相关题目
20.计算($\sqrt{3}$+2)2013($\sqrt{3}$-2)2014的结果是( )
| A. | 2+$\sqrt{3}$ | B. | $\sqrt{3}$-2 | C. | 2-$\sqrt{3}$ | D. | $\sqrt{3}$ |
 图中有8个三角形和9个平行四边形.
图中有8个三角形和9个平行四边形.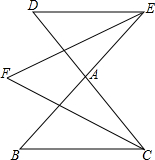 如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.
如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线. 如图,点A关于x轴的对称点的坐标是(5,3).
如图,点A关于x轴的对称点的坐标是(5,3).