题目内容
13.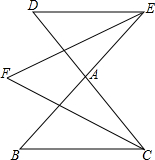 如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.
如图,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.(1)试探求:∠F与∠B、∠D之间的关系?
(2)若∠B:∠D:∠F=2:4:x.求x的值.
分析 (1)先根据角平分线的定义得到∠1=∠2,∠3=∠4,再根据对顶角相等和三角形内角和定理得到∠D+∠1=∠F+∠3,∠B+∠4=∠F+∠2,然后把两式相加即可得到∠F与∠B、∠D之间的关系;
(2)设∠B=2a,则∠D=4a,∠F=ax,利用(1)中的结论得到2ax=2a+4a,然后解关于x的方程即可.
解答 解:(1)∵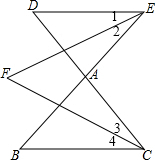 CF为∠BCD的平分线,EF为∠BED的平分线,
CF为∠BCD的平分线,EF为∠BED的平分线,
∴∠1=∠2,∠3=∠4,
∵∠D+∠1=∠F+∠3,
∠B+∠4=∠F+∠2,
∴∠B+∠D+∠1+∠4=2∠F+∠3+∠2,
∴∠F=$\frac{1}{2}$(∠B+∠D);
(2)当∠B:∠D:∠F=2:4:x时,设∠B=2a,则∠D=4a,∠F=ax,
∵2∠F=∠B+∠D,
∴2ax=2a+4a
∴2x=2+4,
∴x=3.
点评 本题考查了三角形内角和定理:通过三角形内角和为180°列等量关系.也考查了角平分线的定义.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
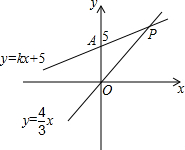 如图,在平面直角坐标系中,一次函数y=kx+5的图象与y轴的交点为点A,与正比例函数y=$\frac{4}{3}$x的图象交于点P.
如图,在平面直角坐标系中,一次函数y=kx+5的图象与y轴的交点为点A,与正比例函数y=$\frac{4}{3}$x的图象交于点P.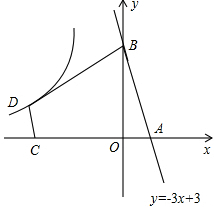 如图,直线l:y=-3x+3与x轴,y轴交于A,B两点,CD∥AB,且AB=3CD,AB⊥BD,BD⊥CD,双曲线y=$\frac{k}{x}$过D点,求k的值.
如图,直线l:y=-3x+3与x轴,y轴交于A,B两点,CD∥AB,且AB=3CD,AB⊥BD,BD⊥CD,双曲线y=$\frac{k}{x}$过D点,求k的值.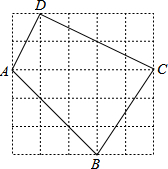 如图,每个小方格都是边长为1的正方形.
如图,每个小方格都是边长为1的正方形.