题目内容
在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1:2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有_____(填序号)
【答案】①②③
【解析】∵∠A+∠B=∠C, ∠A+∠B+∠C=180°,∴2∠C=180°,∠C=90°,∴△ABC是直角三角形;
∵∠A:∠B:∠C=1:2:3,设∠A=x,则x+2x+3x=180,x=30°,∠C=30°×3=90°,∴△ABC是直角三角形;
∵∠A=90°?∠B,∴∠A+∠B=90°,则∠C=180°?90°=90°,∴△ABC是直角三角形;
∵∠A=∠B=∠C,∠A+∠B+∠C=180°, ∴∠A=∠B=∠C=60°,∴△ABC不是直角三角形;
故正确的有①,②,③.
【题型】填空题
【结束】
20
用同样粗细、同种材料的金属线,制作两个全等的△ABC和△DEF.已知∠B=∠E,若AC边的质量为20千克,则DF边的质量为________ 千克.
练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
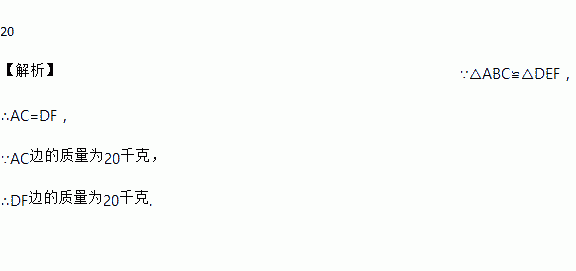

 点的灯泡发出的两束光线
点的灯泡发出的两束光线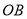 、
、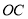 经灯碗反射后平行射出,如果图中
经灯碗反射后平行射出,如果图中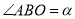 ,
, 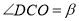 ,则
,则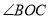 的度数为( ).
的度数为( ).
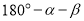 B.
B. 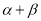 C.
C.  D.
D. 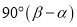
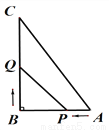

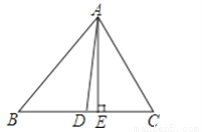
 ∠BAC=35°.
∠BAC=35°.