题目内容
因式分解:
(1)(x2+y2-1)2-4x2y2
(2)a2+b2+2ab-16
(3)x2+5x+6
(4)2x2-3x+1
(5)6x2+5x-6.
(1)(x2+y2-1)2-4x2y2
(2)a2+b2+2ab-16
(3)x2+5x+6
(4)2x2-3x+1
(5)6x2+5x-6.
考点:因式分解-十字相乘法等,因式分解-运用公式法,因式分解-分组分解法
专题:计算题
分析:(1)原式利用平方差公式分解,再利用完全平方公式分解即可;
(2)原式利用完全平方公式变形,再利用平方差公式分解即可;
(3)原式利用十字相乘法分解即可;
(4)原式利用十字相乘法分解即可;
(5)原式利用十字相乘法分解即可.
(2)原式利用完全平方公式变形,再利用平方差公式分解即可;
(3)原式利用十字相乘法分解即可;
(4)原式利用十字相乘法分解即可;
(5)原式利用十字相乘法分解即可.
解答:解:(1)(x2+y2-1)2-4x2y2=(x2+y2+2xy-1)(x2+y2-2xy-1)=(x+y+1)(x+y-1)(x-y+1)(x-y-1);
(2)a2+b2+2ab-16=(a+b)2-16=(a+b+4)(a+b-4);
(3)x2+5x+6=(x+2)(x+3);
(4)2x2-3x+1=(2x-1)(x-1);
(5)6x2+5x-6=(2x+3)(3x-2).
(2)a2+b2+2ab-16=(a+b)2-16=(a+b+4)(a+b-4);
(3)x2+5x+6=(x+2)(x+3);
(4)2x2-3x+1=(2x-1)(x-1);
(5)6x2+5x-6=(2x+3)(3x-2).
点评:此题考查了因式分解-十字相乘法,运用公式法,以及分组分解法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
两个有理数a,b,|a|<|b|,并且a>0,b<0,则下列各式正确的是( )
| A、-a<b<a<-b |
| B、b<-a<a<-b |
| C、-a<-b<b<a |
| D、b<-a<-b<a |
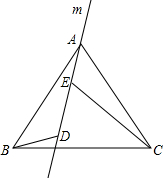 如图,直线m经过正三角形ABC的顶点A,在直线m上取两点D,E,使得使∠ADB=∠AEC=120°.通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明.
如图,直线m经过正三角形ABC的顶点A,在直线m上取两点D,E,使得使∠ADB=∠AEC=120°.通过观察或测量,猜想线段BD,CE与DE之间满足的数量关系,并予以证明.