题目内容
已知函数y=ax2+5x-2的值恒为正数,求a的取值范围.
考点:抛物线与x轴的交点
专题:
分析:当a>0,抛物线的开口向上,如果函数的图象与x轴没有交点,则函数值恒为正数.
解答:解:∵函数y=ax2+5x-2的值恒为正数,
∴△=52-4a×(-2)<0,且a>0,
整理,得
25+8a<0,且a>0,
则a<-
且a>0,
故这样的a不催在.
∴△=52-4a×(-2)<0,且a>0,
整理,得
25+8a<0,且a>0,
则a<-
| 25 |
| 8 |
故这样的a不催在.
点评:本题考查了抛物线与x轴的交点.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系.
△=b2-4ac决定抛物线与x轴的交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;
△=b2-4ac=0时,抛物线与x轴有1个交点;
△=b2-4ac<0时,抛物线与x轴没有交点.
△=b2-4ac决定抛物线与x轴的交点个数.
△=b2-4ac>0时,抛物线与x轴有2个交点;
△=b2-4ac=0时,抛物线与x轴有1个交点;
△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 在△ABC中,BE是∠ABC的平分线,交AC于点E,AD⊥BE,垂足为D,求证:∠BAD=∠C+∠DAC.
在△ABC中,BE是∠ABC的平分线,交AC于点E,AD⊥BE,垂足为D,求证:∠BAD=∠C+∠DAC.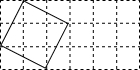 如图,一个矩形由3×6的正方形网格组成,上有4条横线和7条竖线,称为网格的网线;这些网线之间有28个交叉点,称为网格的节点,以节点为顶点,边在网线上的正方形称为网线正方形;以节点为顶点,边不在网线上的正方形称为非网线正方形,图中已经画出了一个非网线正方形.那么,在图上能够画出的非网线正方形共有
如图,一个矩形由3×6的正方形网格组成,上有4条横线和7条竖线,称为网格的网线;这些网线之间有28个交叉点,称为网格的节点,以节点为顶点,边在网线上的正方形称为网线正方形;以节点为顶点,边不在网线上的正方形称为非网线正方形,图中已经画出了一个非网线正方形.那么,在图上能够画出的非网线正方形共有