题目内容
 在△ABC中,BE是∠ABC的平分线,交AC于点E,AD⊥BE,垂足为D,求证:∠BAD=∠C+∠DAC.
在△ABC中,BE是∠ABC的平分线,交AC于点E,AD⊥BE,垂足为D,求证:∠BAD=∠C+∠DAC.考点:三角形的外角性质,直角三角形的性质
专题:
分析:根据角平分线的定义可得∠ABE=∠CBE,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠AED=∠CBE+∠C,然后根据直角三角形两锐角互余列出等式解答即可.
解答:解:∵BE是∠ABC的平分线,
∴∠ABE=∠CBE,
由三角形的外角性质得,∠AED=∠CBE+∠C,
∵AD⊥BE,
∴∠ABE+∠BAD=90°,
∠DAC+∠AED=∠DAC+∠CBE+∠C=90°,
∴∠BAD=∠C+∠DAC.
∴∠ABE=∠CBE,
由三角形的外角性质得,∠AED=∠CBE+∠C,
∵AD⊥BE,
∴∠ABE+∠BAD=90°,
∠DAC+∠AED=∠DAC+∠CBE+∠C=90°,
∴∠BAD=∠C+∠DAC.
点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,直角三角形两锐角互余的性质,熟记性质并准确识图是解题的关键.

练习册系列答案
相关题目
 如图所示,AB=AD,AC=AE,∠DAB=∠CAE,BE与DC交于点P.求证:PA平分∠DPE.
如图所示,AB=AD,AC=AE,∠DAB=∠CAE,BE与DC交于点P.求证:PA平分∠DPE.
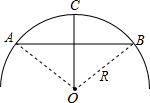 如图,在残破的圆形的轮片图中,弦AB=24cm,半径OC⊥AB于D,CD=4cm,求原轮片的直径.
如图,在残破的圆形的轮片图中,弦AB=24cm,半径OC⊥AB于D,CD=4cm,求原轮片的直径.