题目内容
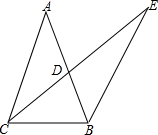
 如图,平行四边形ABCD和平行四边形EAFC的顶点D,B,E,F在同一条直线上,求证:△ABF≌△CDE.
如图,平行四边形ABCD和平行四边形EAFC的顶点D,B,E,F在同一条直线上,求证:△ABF≌△CDE.考点:平行四边形的性质,全等三角形的判定
专题:证明题
分析:因为四边形ABCD是平行四边形,所以可得AB=CD,AB∥CD,进而可得∠CDE=∠ABF,再由四边形EAFC是平行四边形可得∠AFB=∠CED,继而证明可证明△ABF≌△CDE.
解答:证明:∵在平行四边形ABCD中,AB=CD,AB∥CD
∴∠CDE=∠ABF,
∵在平行四边形EAFC中,EC∥AF,
∴∠AFE=∠CEF,
∴∠AFB=∠CED,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(AAS).
∴∠CDE=∠ABF,
∵在平行四边形EAFC中,EC∥AF,
∴∠AFE=∠CEF,
∴∠AFB=∠CED,
在△ABF和△CDE中,
|
∴△ABF≌△CDE(AAS).
点评:本题考查了平行四边形的性质以及全等三角形的判定,解题的关键是熟记平行四边形的各种性质以及全等三角形的各种判定方法.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
已知a、b、c是满足a2+2b=7,b2-2c=-1,c2-6a=-17,则a-b+c的值等于( )
| A、5 | B、4 | C、3 | D、2 |
若多项式x2+kx+4是一个完全平方式,则k的值是( )
| A、2 | B、4 | C、±2 | D、±4 |
-2-1=( )
| A、-1 | B、1 | C、3 | D、-3 |
 如图所示,在长为5cm,宽为3cm的长方形内部有一平行四边形,则平行四边形的面积为( )
如图所示,在长为5cm,宽为3cm的长方形内部有一平行四边形,则平行四边形的面积为( )| A、7cm2 |
| B、8cm2 |
| C、9cm2 |
| D、10cm2 |
 如图,已知AC=AB,AD=5,DB=4,∠A=2∠E.则CD•DE=
如图,已知AC=AB,AD=5,DB=4,∠A=2∠E.则CD•DE=