Question

如图，等边△OBC的边长为10，点P沿O→B→C→O的方向运动，⊙P的半径为

3

，⊙P运动一圈与△OBC的边相切多少次？每次相切时，点P分别在什么位置？

Answer 1

考点：直线与圆的位置关系

专题：计算题

分析：当点P在OB上且与边OC相切时，如图，作PH⊥OC于H，根据直线与圆相切的判定得到PH=

3

，再根据等边三角形的性质得∠O=60°，在Rt△OPH中，利用含30度的直角三角形三边的关系得到OH=

3

3

PH=1，OP=2OH=2，即点P在OB，OP=2时，⊙P与边OC相切，然后利用同样的方法可得BP=2或CP=2时，⊙P与△OBC的边相切．

解答：解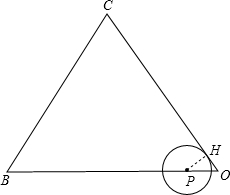：当点P在OB上且与边OC相切时，如图，
作PH⊥OC于H，则PH=

3

，
∵△OBC为等边三角形，
∴∠O=60°，
在Rt△OPH中，OH=

3

3

PH=

3

3

•

3

=1，
OP=2OH=2，
∴点P在OB，OP=2时，⊙P与边OC相切，
同理可得点P在OB，BP=2时，⊙P与边BC相切；
点P在BC，BP=2时，⊙P与边OB相切，
点P在BC，CP=2时，⊙P与边OC相切，
点P在OC，CP=2时，⊙P与边BC相切，
点P在OC，OP=2时，⊙P与边OB相切，
综上所述，⊙P运动一圈与△OBC的边相切6次，每次相切时，点P分别距离△OBC的顶点2个单位．

点评：本题考查了直线和圆的位置关系：设⊙O的半径为r，圆心O到直线l的距离为d．直线l和⊙O相交?d＜r；直线l和⊙O相切?d=r；直线l和⊙O相离?d＞r．也考查了等边三角形的性质．