题目内容
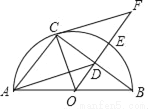
如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D,点F为OE的延长线上一点且OC2=OD•OF.
(1)求证:CF为⊙O的切线.
(2)已知DE=2,tan∠BAC=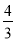 .
.
①求⊙O的半径;
②求sin∠BAD的值.
练习册系列答案
相关题目
题目内容
如图,AB是半圆O的直径,E是弧BC的中点,OE交弦BC于点D,点F为OE的延长线上一点且OC2=OD•OF.
(1)求证:CF为⊙O的切线.
(2)已知DE=2,tan∠BAC=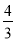 .
.
①求⊙O的半径;
②求sin∠BAD的值.
